どこよりも遅い!数学2B第5問 解説
最終更新日2008年2月23日
下の表は、10名からなるある少人数クラスを I 班と II 班に分けて、100点満点で2回ずつ実施した数学と英語のテストの得点をまとめたものである。ただし、表中の平均点はそれぞれ1回目と2回目の数学と英語のクラス全体の平均点を表している。また、A,B,C,Dの値は全て整数とする。
| 1回目 | 2回目 | ||||
| 班 | 番号 | 数学 | 英語 | 数学 | 英語 |
| I | 1 | 40 | 43 | 60 | 54 |
| 2 | 63 | 55 | 61 | 67 | |
| 3 | 59 | B | 56 | 60 | |
| 4 | 35 | 64 | 60 | 71 | |
| 5 | 43 | 36 | C | 80 | |
| II | 6 | A | 48 | D | 50 |
| 7 | 51 | 46 | 54 | 57 | |
| 8 | 57 | 71 | 59 | 40 | |
| 9 | 32 | 65 | 49 | 42 | |
| 10 | 34 | 50 | 57 | 69 | |
| 平均値 | 45.0 | E | 58.9 | 59.0 | |
〔1〕1回目の数学の得点について、I 班の平均点は(アイ).(ウ)点である。また、クラス全体の平均点は45.0点であるので、II 班の1番目の生徒の数学の得点Aは(エオ)点である。
〔2〕II 班の1回目の数学と英語の得点について、数学と英語の分散はともに101.2である。したがって、相関係数は(カ).(キク)である。
〔3〕1回目の英語の得点について、I 班の3番目の生徒の得点Bが分からないとき、クラス全体の得点の中央値Mの値として(ケ)通りの値があり得る。
実際は、1回目の英語の得点のクラス全体の平均点Eが54.0点だった。したがって、Bは(コサ)点となり、中央値Mは(シス).(セ)点である。
〔4〕2回目の数学の得点について、I 班の平均点はII 班の平均点より4.6点大きかった。したがって、I 班の5番目の生徒の得点Cから II 班の1番目の生徒の得点Dを引いた値は(ソ)点である。
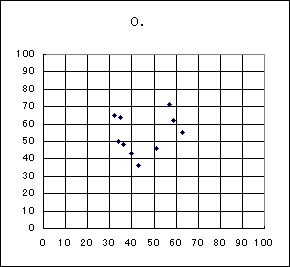
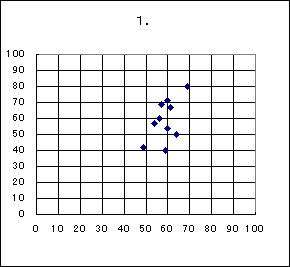
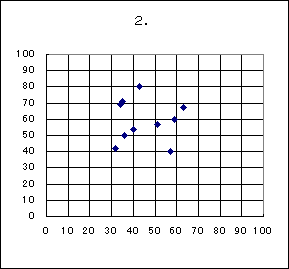
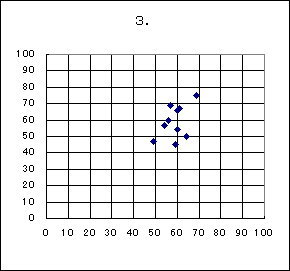
〔5〕 1回目のクラス全体の数学と英語の得点の相関図(散布図)は、(タ)であり、2回目のクラス全体の数学と英語の得点の相関図は、(チ)である。また、1回目のクラス全体の数学と英語の得点の相関係数を r 1, 2回目のクラス全体の数学と英語の得点の相関係数を r2 とすると値の組 (r1, r2) として正しいのは(ツ)である。(タ)(チ)に当てはまるものを、それぞれ次の0〜3のうちから一つずつ選べ。

|

|

|

|
| 0.(0.54, 0.20) | 1.(-0.54, 0.20) |
| 2.(0.20, 0.54) | 3.(0.20, -0.54) |
0.変更前より減少 1.変更前と一致 2.変更前より増加
解答
(1) 1回目のI班の数学の得点の平均は(40+63+59+35+43)/5 = 240/5 = 48.0
クラス全員の平均が45.0点であることから II 班の得点の合計は45.0×10−240=210
よってAの値は210−(51−57−32−34) = 36 点
(2) II 班の1回目の数学と英語の得点の各教科の平均と各得点の平均との差を計算すると次のようになる。
| I 班 | II 班 | 2つの (得点−平均) の積 | ||
| 得点 | 得点−平均 | 得点 | 得点−平均 | |
| 36 | -6 | 48 | -8 | 48 |
| 51 | 9 | 46 | -10 | -90 |
| 57 | 15 | 71 | 15 | 225 |
| 32 | -10 | 65 | 9 | -90 |
| 34 | -8 | 50 | -6 | 48 |
| 平均 | 平均 | 上の5つの合計 | ||
| 42 | 56 | 141 | ||
141/(101.2*5) ≒ 0.28
(3)10人の得点の中央値は、得点を高い順に並べたとき、5番目と6番目の平均になる。1回目の英語のB以外9人の得点を得点の高い順に並べたとき4番目:55点、5番目:50点、6番目:48点
となる。Bは整数であるため、中央値について次の可能性がある。
| Bの範囲 | 5番目 | 6番目 | 中央値 |
| B≧55 | 50 | 55 | 52.5 |
| 50≦B≦54 | 50 | B | B/2+50 |
| B=49 | 49 | 50 | 49.5 |
| B≦48 | 48 | 50 | 49 |
−11、1、B−54、10、−18、−6、−8、17、11、−4
となる。平均値が54.0であるため、これら10個の値の合計は0でなければいけない。10個の値の合計は B−62 となるため、B=62である。このことから中央値は上の表から52.5点となる。2回目の英語の I 班の得点から60点を引いた値を番号順に並べると
0、1、−4、0、C−60
2回目の英語の II 班の得点から60点を引いた値を番号順に並べるとD−60、−6、−1、−11、−3
I 班の平均点と II 班の平均点の差は上の各5つの値の平均の差と等しい。これより
(0+1−4+0+C−60)/5−(D−60−6−1−11−3)/5
=4.6
⇒(C−63)−(D−81)=23
⇒C−D=5
0.の相関図は全体にばらつきがあるため、相関係数は0に近い。一方1.の相関図は正の相関があるため、1に近い。これより (r1, r2) として正しいのは2.の(0.20,0.54)となる。
(6) 2回目のクラス全員10名の英語の得点について、得点の高い2名の得点が2点ずつ下がり、得点の低い2名の得点が2点ずつあがった。そのほか6名の得点に変更はなかった。
このとき、10人の合計得点は2点あがり、2点下がったため、増減はない。よって平均点も変更前と一致する(選択肢1.)
一方、分散については、平均値から最も離れている4名の得点が変更により平均値に近づいたため、分散は変更前より減少する(選択肢0.)
数学とクイズでくつろいで<数学の部屋<どこよりも遅い!センター試験数学 解説<数学2B第5問 解説