どこよりも遅い!数学2B第5問 解説
最終更新日2007年3月8日
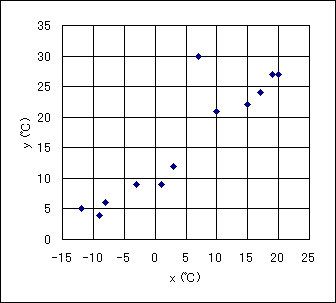
ある都市のおけるある年の月ごとの最低気温を変量 x、最高気温を変量 y とする。ただし単位は℃とし、最低気温と最高気温は、一日の最低気温と最高気温について月ごとに平均をとり、小数第1位を四捨五入したものとする。次の図は、変量xと変量yの相関図(散布図)である。

〔1〕1月から12月までの変量 x は次の通りであった。
−12, −9, −9, 3, 10, 17, 20, 19, 15, 7, 1, −8
この12個の値の平均値は(ア).(イ)℃。中央値は(ウ).(エ)℃である。〔2〕1月から12月までの12ヶ月を、変量 x が0℃未満の四つの月からなるAグループと、0℃以上の八つの月からなるBグループとに分けて分析した。
このとき、Aグループにおける変量 x の平均値は(オカ).(キ)℃であり、分散は(クケ).(コ)である。
また、Aグループにおける変量 y の平均値は6.0℃で、Bグループにおける変量 y の平均値は21.5℃であった。このとき、1月から12月までの変量 y の平均値は(サシ).(ス)℃である。
変量 x と変量 y の相関図のデータの中で、入力ミスが見つかった。変量 x の値が7℃、変量 y の値が30℃となっている月の変量 y の値は、正しくは18℃であった。
〔3〕この誤りを修正すると、変量 y の平均値は(セ),(ソ)℃減少する。また、変量 y の分散は(タ)する。ただし、(タ)については、当てはまるものを次の0〜2のうちから一つ選べ。
0.修正前より増加 1.修正前より減少 2.修正前と一致
〔4〕修正前の変量 y の中央値は(チ)℃であるが、修正後には変量 y の中央地は(ツ)℃となる。(チ)、(ツ)の数値として適当なものを、相関図を参考にして、次の0〜3のうちから一つずつ選べ。0 … 13.5、1 … 15.0、2 … 16.5、3 … 18.0
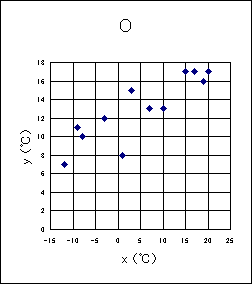
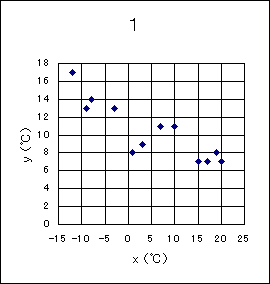
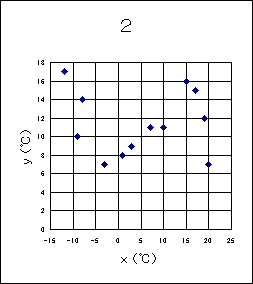
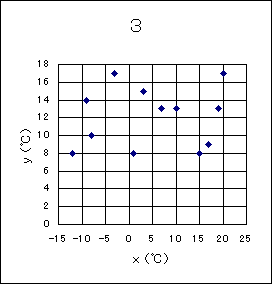
〔5〕 誤りを修正した後の寒暖の差(最高気温と最低気温の差)を変量 z (=y-x)とする。変量 z の平均値は(テト).(ナ)℃であり、変量 x と変量 z の相関図として適当なものは(ニ)である。ただし、(ニ)については、当てはまるものを次の0〜3のうちから一つ選べ。
|
|
|
|
|
0 … 正の相関があり、最低気温が高い月ほど寒暖の差が大きい 1 … 正の相関があり、最低気温が低い月ほど寒暖の差が大きい 2 … 負の相関があり、最低気温が高い月ほど寒暖の差が大きい 3 … 負の相関があり、最低気温が低い月ほど寒暖の差が大きい 4 … 相関関係はほとんどなく、最低気温によって寒暖の差は影響を受けない |
解答
1月から12月までの変量 x の値の合計は 60 となるため平均値は60/12=5.0℃。また変量 x を小さい順に並べた場合、6番目は3、7番目が7 となることから中央値は(3+7)/2=5.0℃になる。変量 x が0℃未満の四つの月からなるAグループの値の合計は−32となることから平均値は−32/4=−8.0℃。一方、各変量 x と平均値との差は−4、−1、5、0 となることから各値の平方の和は16+1+25+0=42。よって分散は42/4=10.5
また、Aグループにおける変量 y の平均値は6.0℃で、Bグループにおける変量 y の平均値は21.5℃であるとき、Aグループにおける変量 y の合計は6.0×4=24.0、Bグループにおける変量 y の合計は21.5×8=172.0
よって1月から12月までの変量 y の値の合計は24+172=196となり、12ヶ月の平均値は196/12≒16.3℃
変量 x の値が7℃、変量 y の値が30℃となっている月の変量 y の値は、正しくは18℃であった。つまり変量 y の値の合計は30−18=12℃減少する。このため平均値も12/12=1.0℃減少する。つまり平均値は16.3−1.0=15.3℃になる。また修正後の各変量 y の値は平均値に近い値となるため分散は修正前より減少することが分かる。 問題の選択肢では1にあたる。
修正前の変量 y を小さい順に並べた場合、6番目はおよそ12℃、7番目が21℃ となることから中央値は(12+21)/2=16.5℃(問題の選択肢では2)になる。一方、修正後の変量 y を小さい順に並べた場合、6番目はおよそ12℃、7番目が18℃ となることから中央値は(12+18)/2=15.0℃(問題の選択肢では1)になる。
変量 z を z=y-x とした場合、
(変量 z の平均値)=(変量 y の平均値)−(変量 x の平均値)
が成り立つ。変量 y の平均値は(3)の問題から15.3℃。変量 x の平均値は問題(1)から5.0℃であることから、変量 z の平均値は10.3℃となる。変量 x と変量 y の相関図で左下の値を見ると(x, y)=(−12,5)、(−9,4)となる点がある。 これらから変量 x と変量 z の相関図には(x, z)=(−12,17)、(−9,13)に点を打つ必要がある。問題の選択肢の中でこの2点を打っているのは1の相関図である。
1の相関図は変量 x の値が高いほど変量 z の値は低くなる。これは最低気温 x と寒暖の差 z について負の相関があり、最高気温が低い月ほど寒暖の差が大きいことを示している。問題の選択肢では3にあたる。
数学とクイズでくつろいで<数学の部屋<どこよりも遅い!センター試験数学 解説<数学2B第5問 解説