数学とクイズでくつろいで＜数学の部屋＜どこよりも遅い！センター試験数学 解説＜工業関係基礎 第３問 解説

どこよりも遅い！工業関係基礎 第３問 解説

最終更新日２０１０年１０月２６日

導体の温度の変化に伴う電気抵抗の変化や、その応用について考える。

問１

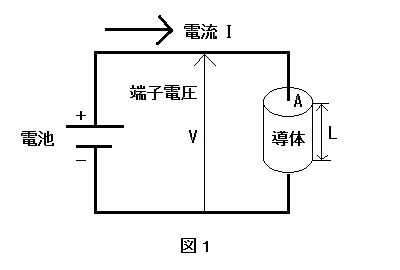
　図１のように、長さ L [m]、断面積 A [m^2] の導体の両端面に電池を接続する。ここで、電池と導体をつなぐ接続線の抵抗は、 導体の抵抗に比べて非常に小さく無視できるものとする。このとき導体に流れる電流 I [A]、電子電圧 V [V]、抵抗 R [Ω] の間には、オームの法則 つまり V = RI の関係が成立する。

　導体の抵抗は、導体の材質や形状によって異なる。長さ L [m]、断面積 A [m^2] の導体の抵抗 R [Ω] は次の式で表される。

R = ρ（L/A）…… (1)

ここで、ρ [Ω・m] は抵抗率と呼ばれ、長さ１m、断面積１m^2の導体の両端面間の抵抗に相当する。

　ある合金の棒について、断面が一辺 2.0 mm の正方形で長さ 0.80 m とする。抵抗率が 1.4×10^(-6) Ω・m ならば 断面積が (2.0)^2 [mm^2] = (2.0 × 10^(-3) )^2 [m^2] であるため式 (1) からこの棒の抵抗は

1.4 × 10^(-6) × (0.80 / (2.0 × 10^(-3) )^2) = 1.4 × 0.80 / 4.0 = 0.28 Ω

となる。

　温度が S [℃] のときの抵抗が R_s [Ω]、T [℃] のときの抵抗が R_t [Ω] の導体を考える。T > S の関係があり、この温度範囲において、 温度の変化に対する抵抗の変化率は一定であるとする。このとき次の式が成り立つ。

R_t = R_s｛ 1＋α (T-S) ｝…… (2)

ここで、α [/℃] は S [℃] の時の抵抗温度係数と呼ばれる。この式を変形すると

となる。右辺の値は 1 ℃当たりの抵抗の変化量である。

　気温 20 ℃の部屋で 40 W の白熱電球の電気スタンドを点灯させる。電気スタンドの電球以外の抵抗は無視する。100 V の電源につなぎ電球を点灯させて、しばらくすると明るさが一定になった。
　このとき電球内で発光しているフィラメントは 40 W の電力を消費する。電球にかかる電圧 V [V], 電球に流れる電流 I [A], 電球で消費される電力 P [W]　の間には、P = VI の関係が成立するから、フィラメントに流れる電流は

40 = 100 × I ⇒　I = 0.40 A （解答群の９．）

ということになる。したがって、フィラメントの抵抗はオームの法則から

R = V/I = 100 / 0.40 = 250 Ω （解答群の５．）

である。このときのフィラメントの温度は 2.4 × 10^3 ℃であった。

　20 ℃のときのフィラメントの抵抗温度係数αは 4.6 × 10^(-3) /℃ である。温度が 20 ℃ から 2.4 × 10^3 ℃ までの範囲で式 (2) が成立するものとすれば 20 ℃ における点灯前の電球の抵抗は

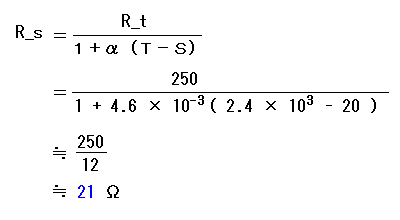
　点灯後の電球の抵抗は点灯前の電球の抵抗の１０倍以上になっている。つまり点灯前の電流は点灯後の電流の１０倍以上となる。 電球の寿命はこのような点灯・消灯による電流の大きな変化が影響している。

問２

　図２はブリッジ回路と呼ばれる回路である。それぞれの部分は以下の通り。

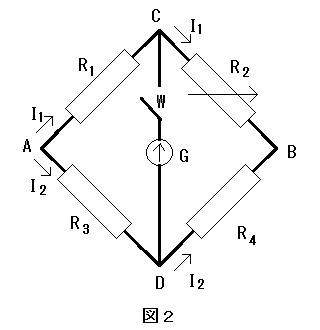
図の AB 間に電圧をかけてスイッチＷを閉じると、検流計にも電気が流れることがある。検流計の指針が振れなくなったとき CD 間に電流が流れていない。このときブリッジ回路は平衡しているという。

　スイッチ W を開いて AB 間に電圧 V [V] をかけると、R_1 と R_2 に流れる電流 I_1 [A] はオームの法則から

I_1 = V × 1/(R_1 + R_2)（解答群の０．）

同じく R_3 と R_4 に流れる電流 I_2 [A] は I_2 = V × 1/(R_3 + R_4)（解答群の１．）となる。
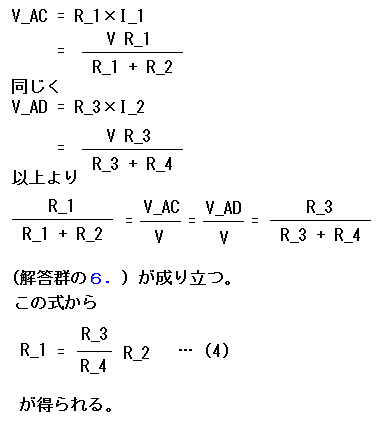
　スイッチ W を閉じても検流計の指針が振れないように可変抵抗 R_2 を調整すれば、AC 間の電圧 V_{AC} [V] と AD間の電圧 V_{AD} [V] は等しくなり、 ブリッジ回路は平衡する。このとき、

となる。

　ブリッジ回路を使い、白金の抵抗温度係数を求める。ブリッジ回路の抵抗 R_1 として、温度が 10 ℃のときの抵抗が 20 Ωの白金をつなぐ。温度が 10 ℃のとき、R_2 = 1.0 kΩ で平衡した。次に白金の温度のみを 3.1 × 10^2 ℃ に上昇させたとき、R_2 = 2.1 kΩ で平衡した。上の式 (4) を使うと

式 (2) を用いて 10 ℃における白金の抵抗温度係数を求めると

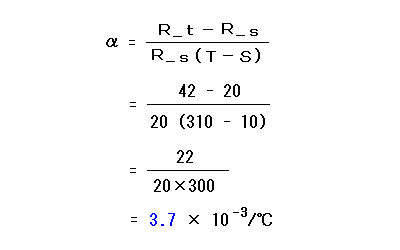
問３

　図３のようなブリッジ回路を考える。それぞれの部分は以下の通り。

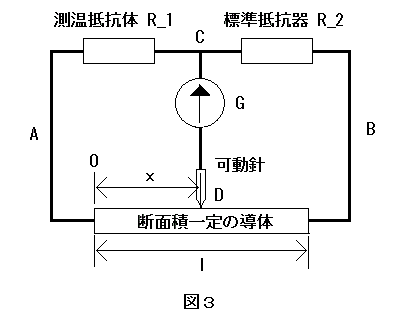
ここでは導体として、断面が一辺 2.0 mm の正方形で長さが l = 0.80 m, 抵抗率が 1.4×10^(-6) Ω・m の合金の棒を用いる。 棒の端点 O から可動針の先端 D までの長さ x [m] を正確に測定し、その地点で接触しているものとする。このとき問２の図２の回路と対比すると、R_3 は長さ x [m] の合金の棒、R_4 は長さ (l-x) [m] の合金の棒の各抵抗に等しい。R_2 と合金の棒はそれぞれ一定の温度に保たれているとする。

　図２のブリッジ回路が平衡するとき、式 (4) が成り立つ。このことから図３では l, x を使って

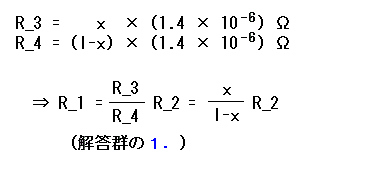
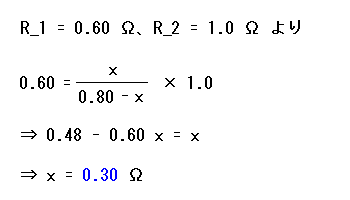
標準抵抗器の抵抗値が 1.0 Ω, 20 ℃ での測温抵抗体の抵抗値が 0.60 Ωならば、上の式を使い回路が平衡するときの可動針の位置 x を求めると

回路の測温抵抗体をオーブン内に入れた状況を考える。可動針が x/l = 0.55 の位置に移動したとき、ブリッジ回路が平衡した。 測温抵抗体の抵抗温度係数αを 4.5 × 10^(-3) /℃ とし、式 (2) を用いてオーブン内の温度を求める。

数学とクイズでくつろいで＜数学の部屋＜どこよりも遅い！センター試験数学 解説＜工業関係基礎 第３問 解説