どこよりも遅い!数学2B第5問 解説
最終更新日2008年2月23日
次の表は、高等学校のある部に入部した20人の生徒について、右手と左手の握力(単位 kg)を測定した結果である。測定は10人ずつの二つのグループについて行われた。ただし、表中の数字はすべて正確な値であり、四捨五入はされていないものとする。
第1グループ
|
第2グループ
|
〔1〕第1グループに属する10人の右手の握力について、平均値Aは(アイ).(ウ)kg である。
また、20人全員の右手の握力について、平均値Mは(エオ).(カ)kg, 中央値は(キク).(ケ)である。
〔2〕右手の握力について、20人全員の平均値Mからの偏差の2乗の和を、2つのグループそれぞれについて求めると、第1グループでは(コサシ)であり、第2グループでは420である。したがって、20人全員の右手の握力について、標準偏差Sの値は(ス).(セ)kg である。
〔3〕tを正の実数とする。20人全員の右手の握力の平均値Mと標準偏差Sを用いて、M−tS よりおおきく M+ts より小さい範囲を考える
20人全員の中で、右手の握力の値がこの範囲に入っている生徒の人数を N(t) とするとき、N(1)=(ソタ)であり、N(2)=(チツ)である。
〔4〕第2グループに属する10人の左手の握力について、平均値Dは(テト).(ナ)kg であり、中央値が 40.5 kg であるから、Bの値は(ニヌ)kg, Cの値は(ネノ)kg である。ただし、Bの値はCの値より大きいものとする。これより、EとFの値も定まる。
〔5〕20人の各生徒について、右手と左手の握力の平均値と、右手と左手の握力の差の絶対値を求めた。握力の平均値については、最初にあげた表の「左右の握力の平均値」の列に示してある。
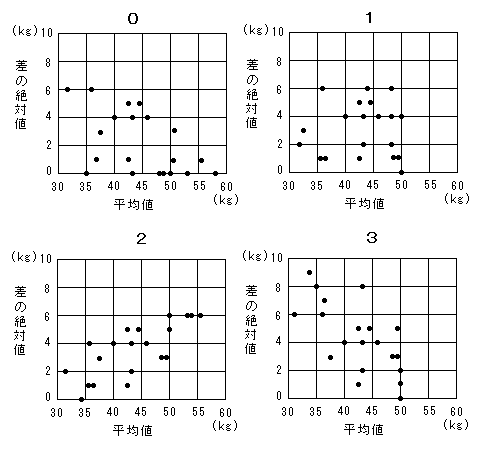
握力の平均値を横軸に、握力の差の絶対値を縦軸にとった相関図(散布図)として適切なものは(ハ)であり、相関係数の値は(ヒ)に最も近い。したがって、この20人については、(フ)。(ハ)に当てはまるものを、それぞれ次の0〜3のうちから一つ選べ。

|
| 0: −0.9 | 1: −0.5 | 2: 0.0 | 3: 0.5 | 4: 0.9 |
0.握力の平均値が増加するとき、握力の差の絶対値が増加する傾向が認められる。
1.握力の平均値が増加するとき、握力の差の絶対値が増加する傾向も減少する傾向も認められない。
2.握力の平均値が増加するとき、握力の差の絶対値が減少する傾向が認められる。
解答
[1]第1グループの右手の握力の合計を R1、左手の握力の合計を L1とおくとR1/10 = A,L1/10 = 44.5,(R1 + L1)/20 = 44.75
このことからL1 = 44.5×10 = 445, R1 + L1 = 44.75×20 = 895 ⇒ R1 = 895 - 445 = 450
となるため A = 450/10 = 45.0 kg第2グループの右手の握力の合計を R2、左手の握力の合計を L2とおくと同様の計算により
R2 = 43.0×10 = 430
となるため、20人全員の右手の握力の平均値 M はM = (R1 + R2)/20 = (450 + 430)/20 = 44.0 kg
また、20人全員の右手の握力を値の大きい順に並べていくと10番目:46 kg(第1グループの番号3番) 11番目:45 kg(第2グループの番号18、19番)
であるため、中央値はこの2つの値の平均 (46+45)/2 = 45.5 kg となる。[2] 右手の握力について、20人全員の平均値 M = 44.0 からの偏差の2乗の和を、2つのグループそれぞれについて求めると以下のようになる。
| 第1グループ | 第2グループ | ||
| 番号 | (握力−M)^2 | 番号 | (握力−M)^2 |
| 1 | 25 | 11 | 169 |
| 2 | 49 | 12 | 121 |
| 3 | 1 | 13 | 16 |
| 4 | 9 | 14 | 4 |
| 5 | 4 | 15 | 49 |
| 6 | 100 | 16 | 25 |
| 7 | 9 | 17 | 25 |
| 8 | 4 | 18 | 1 |
| 9 | 25 | 19 | 1 |
| 10 | 64 | 20 | 9 |
| 合計 | 290 | 合計 | 420 |
(290+420)/20 = 710/20 = 35.5
となるため、標準偏差はこの分散の平方根、約 S=6.0 となる。[3]M = 44.0, S=6.0 より N(1) は右手の握力が 44.0-6.0 = 38.0 より大きく 44.0+6.0 = 50.0 より小さい値の人数となる。表からこの範囲の人数を数えると N(1)=12となる。同様に N(2) は右手の握力が 44.0-2×6.0 = 32.0 より大きく 44.0+2×6.0 = 56.0 より小さい値の人数となるため、N(2)=19となる。
[4][1]の計算と同様にして考えると
R2/10 = 43.0, L2/10 = D, (R2 + L2)/20 = 41.25
このことからR2 = 43.0×10 = 430, R2 + L2 = 41.25×20 = 825 ⇒ L2 = 825 - 430 = 395
よって D = 395/10 = 39.5B + C = 395 - 308 = 87
また中央値が 40.5 kg であるため、40 kg と 41 kg がデータの中にある必要がある。 41 kg は表にあるが 40 kg は表にないため、B, C のいずれかは 40 kg でなければいけない。このため(B, C) = (40, 47) または (47, 40)
Bの値はCの値より大きいことから B = 47 kg, C = 40 kg.[4]20人の左右の手の握力について
左右の握力が同じ値(差の絶対値が0)であるのは第1グループ9番の人で、握力は共に 50 kg.
左右の握力の平均値が 50.0 kg であるのは第1グループの2番、9番の2人。
以上2つの条件を満たす相関図は(1)のみである。
この相関図には増加の傾向も減少の傾向も見られないため、相関係数は2.の 0.0 に近く、この20人について握力の平均値が増加するとき、握力の差の絶対値が増加する傾向も減少する傾向も認められない(解答群の1.)
数学とクイズでくつろいで<数学の部屋<どこよりも遅い!センター試験数学 解説<数学2B第5問 解説