問題：たろうくんは１から順に１，２，３…とある数までを黒板に書きました。 じろうくんはその中の１個の数を消してしまいました。すると残りの数の平均は５９０／１７になりました。 じろうくんの消した数はいくつですか？

見たことあるけど解いたことのない問題

解いたことあるけど解き方を覚えていない問題です。

　「執行猶予が消えました！」と明るいオチで答えた（悲しいことに大笑いしてしまいました）バンビーノ小林率いる（？）コマ大チーム。今回は「駄菓子バー」という店で検証を行った。ここは５００円で駄菓子が食べ放題、とコマ大検証には打ってつけの店。この駄菓子ベスト１００から１個ずつ選びその順位を「消した数」として正解か検証を行った。
　一つずつ検証するが答えの平均値に近づく気配なし。ここでアタルチャンス！黒板に書いた数字が「１から１００まで」と考えていたのが間違いではないのか、ということで数字を減らして検証を続ける。それに対して悲鳴を上げ始めたのがコマ大チームのお腹。たかが駄菓子、しかし食べ続けるとさすがに満腹になる。考えると「検証だけなら食べなきゃいいんじゃないの」と思ったが、それでも食べ続け、検証時間２時間半、どうにか答えを出した。

　私もいつものようにコマ大チームの検証を見ながら解いていったが、もう一歩のところで答えが見つからず…

残りの数の平均は （１から「ある数」までの和−「消えた数」）／（ある数−１） と書くことができる。問題ではこの平均は「５９０／１７」となっているが、約分された可能性もあるため、 分子：（１から「ある数」までの和−「消えた数」）＝５９０ｋ 分母：（「ある数」−１）＝１７ｋ と書くことができる。このことから 「ある数」＝１７ｋ＋１ 「消えた数」＝（１から「ある数」までの和）−５９０ｋ となる。ｋ＝１，２，３… と順番に数字を入れていくと ｋ ある数 １から「ある数」までの和 （１から「ある数」までの和）−５９０ｋ （＝「消えた数」？） １ １８ 　１＋２＋…＋１８ ＝１８×１９／２ ＝１７１ 　１７１−５９０×１ ＝−４１９ ２ ３５ 　１＋２＋…＋３５ ＝３５×３６／２ ＝６３０ 　６３０−５９０×２ ＝−５５０ ３ ５２ 　１＋２＋…＋５１ ＝５１×５２／２ ＝１３２６ 　１３２６−５９０×３ ＝−４４４ ４ ６９ 　１＋２＋…＋６９ ＝６９×７０／２ ＝２４１５ 　２４１５−５９０×４ ＝５５ ５ ８６ 　１＋２＋…＋８６ ＝８６×８７／２ ＝３７４１ 　３７４１−５９０×５ ＝７９１ ｋ＝１、２、３の場合は消えた数を計算すると０より小さくなってしまう。 一方ｋ＝５の場合は消えた数「７９１」がある数「８６」より大きくなるため条件に 合わない。よってｋ＝４の時の「ある数＝６９、消えた数＝５５」が答えになる。

　東大生チームは「秒殺シスターズ」に負けずとも劣らぬ速さで計算を進め、中村先生の解説が終わるか終わらないかのうちに答えをはじき出した。一方相変わらず苦戦しているマス北野。しかしどうにか答えを出すことができた。

コマ大チーム	５５
東大生チーム
マス北野

正解…もちろん、５５（ある数は６９）

１からｎまでの数字から一つ除いた数の平均の最大値と最小値を考える。 最大の値のときは「１」を取った場合。このとき 　２からｎまでの和 ＝ｎ（ｎ＋１）／２−１ ＝（ｎ−１）（ｎ＋２）／２ ⇒ 　平均値 ＝（（ｎ−１）（ｎ＋２）／２）／（ｎ−１） ＝（ｎ＋２）／２ 一方、最小の値のときは「ｎ」を取った場合。このとき 　１からｎ−１までの和 ＝ｎ（ｎ−１）／２ ⇒ 　平均値 ＝（ｎ（ｎ−１）／２）／（ｎ−１） ＝ｎ／２ このことから ｎ／２≦５９０／１７≦（ｎ＋２）／２　⇒⇒⇒　ｎ＝６８、６９ 分母が１７であることから、ｎ＝１７ｋ＋１という形で書くことができる。これから ｎ＝６９であることが分かる。この後は計算で消えた数が求まる。

東大生チームの答えが見えてしまいました。

問題： 　深い森の奥に妖精の村がありました。妖精はみな、赤色か青色の帽子をかぶっています。しかし、村に何人住んでいるか、赤と青の帽子が何人いるか、自分の帽子が何色か無関心に暮らしていました。そのうえ他人の帽子の色には触れてはならない掟があったのです。 　しかし、自分の帽子の色が分かるときが来ました。百年に一度、青い帽子をかぶった妖精しか参加ができない祭の開催です。誰も自分の帽子の色を知らないので、知らないうちは祭に参加できます。しかし、もし自分が赤い帽子だと分かったら最後、翌日からの参加はできないのです。 　初日は妖精全員が参加しました。集まった妖精は全部で４００人でした。みんな密かに赤い帽子、青い帽子が何人いるか数えてみました。でも掟のため話題にできません。妖精たちは自分の推理で自分の帽子の色を判断しなければならないのです。実はこの祭の初日には青い帽子の妖精が２００人、赤い帽子の妖精が２００人参加していました。もちろん妖精たちは自分以外の帽子の内訳しか分かっていません。 　では、赤い帽子の妖精が祭からいなくなるまで何日間かかるでしょうか？

なんだ、この掟は？
なんだ、この祭は？

　今回のコマ大の検証。検証の前に問題が理解できない、というわけでゲストの方に読んでもらう事にした。

声優「恒松あゆみ」さん…あまりのセクシーボイスのため集中できず。
物まねタレント「ホリ」さん…金八先生などの物まねで問題を朗読したがコマ大チームがはしゃぎすぎたため、最後はテリー伊藤になって怒って退室。
声優「黒田崇矢」さん…深い眠りに導かれたが、どうにか理解できた模様。

は？これだけ？

　シンプルな問題が多いこの番組には珍しい長文の問題。問題文の森の奥や祭や必要ない箇所を省いて次のようにまとめてみます。

問題をまとめたもの： 　４００人の妖精がいます。彼らは赤色か青色の帽子をかぶっています。 　しかし彼らは自分がどちらの色の帽子をかぶっているかは分かりません。 また、他人の帽子の色は知ることができますが、それを他の妖精に話すことはできません。 　この４００人がある日一つの場所に集まりました。彼らは自分以外の全員の帽子の色を知ることができます。ここで 「もし自分の帽子の色が赤色であることが分かったら、その次の日には来ないでください。分からなければ次の日にも来て下さい。」 というルールを決めました。実は４００人のうち赤い帽子の妖精は２００人、青い帽子の妖精は２００人いました。さて赤い帽子の妖精が全員来なくなるのは何日目でしょう？

赤色の帽子、青色の帽子の妖精は必ず一人以上いることは
妖精たちは知っている。

今回も私はすぐに分かりました。

え〜〜い！両方とも書いちゃえ！

私の答え： ２００日目に赤の帽子の妖精が全員帽子の色に気付く ２０１日目に全員青の帽子の妖精だけが祭に参加。

コマ大チーム	２４６日間	「赤」坂と「青」山を通るのは ２４６号線…という理由から？
東大生チーム	２０１日間	赤い帽子の人数が少ない 場合から考えた。
マス北野	４００日間	「赤い帽子の人数×２」の日数が かかると予想して

正解…２０１日間、東大生チーム正解！

それぞれの妖精が見た他の妖精の帽子の色の数を考える。 ・他の妖精の帽子が全員青のとき 妖精から見たところ 「赤の帽子の妖精が一人はいる」ということはその一人は自分であることが分かる。 ⇒⇒⇒この妖精は１日目に自分の帽子が赤であることが分かり 　　　２日目には来ない。 ・他の妖精の帽子が一人が赤、残り全員青のとき 妖精から見たところ もし自分の帽子が青ならば、あの赤の帽子の妖精から見たほかの妖精の帽子の色は「全員青（一つ上の図）」のはず。ということは上の考え方からこの妖精は２日目は来ないはず。 　２日目に赤の帽子の妖精が来ない ⇒⇒⇒自分の帽子の色が青であることが分かる。 　２日目に赤の帽子の妖精が来る。 ⇒⇒⇒自分の帽子の色が赤であることが分かる。 ⇒⇒⇒この妖精は２日目に自分の帽子が赤であることが分かり 　　　３日目には来ない （この妖精の見た赤の帽子の妖精も同じ考え方から３日目には来ない） ・他の妖精の帽子が２人が赤、残り全員青のとき 妖精から見たところ もし自分の帽子が青ならば、あの赤の帽子の２人の妖精から見たほかの妖精の帽子の色は「一人が赤、残り全員青（一つ上の図）」のはず。ということは上の考え方からこの妖精は３日目は来ないはず。 　３日目に赤の帽子の妖精が来ない ⇒⇒⇒自分の帽子の色が青であることが分かる。 　３日目に赤の帽子の妖精が来る。 ⇒⇒⇒自分の帽子の色が赤であることが分かる。 ⇒⇒⇒この妖精は３日目に自分の帽子が赤であることが分かり 　　　４日目には来ない （この妖精の見た赤の帽子の妖精も２人とも同じ考え方から４日目には来ない） この考え方を続けると ・他の妖精の帽子がＮ人が赤、残り全員青のとき もし自分の帽子が青ならば、あの赤の帽子のＮ人の妖精から見たほかの妖精の帽子の色は「（Ｎ−１）人が赤、残り全員青」のはず。ということはこれまでの考え方からこの妖精は（Ｎ＋１）日目は来ないはず。 　（Ｎ＋１）日目に赤の帽子の妖精が来ない ⇒⇒⇒自分の帽子の色が青であることが分かる。 　（Ｎ＋１）日目に赤の帽子の妖精が来る。 ⇒⇒⇒自分の帽子の色が赤であることが分かる。 ⇒⇒⇒この妖精は（Ｎ＋１）日目に自分の帽子が赤であること 　　　が分かり（Ｎ＋２）日目には来ない （この妖精の見た赤の帽子の妖精も全員同じ考え方から（Ｎ＋２）日目には来ない） ということが分かる。今回の問題では赤の帽子の妖精から見た他の妖精の帽子の色は 「１９９人が赤、残り２００人青」となるため、上の考え方から１９９＋２＝２０１日目に赤の帽子の妖精は全員来なくなる。

　今回は文句なしで東大生チームにコマ大フィールズ賞が渡った。それにしても

なんだこの理屈っぽい妖精たちは？

問題：約数の個数が２８個ある最小の自然数ｎを求めなさい。

なー〜−んだ、簡単な問題じゃないか

今回は解けるまでの速さで競っていただきます。

　コマ大チームはダンカン部長が他局のテレビドラマの監督をしているということで今回（と、あと２回）はスタジオ出演はお休み（検証では出演）早稲田の問題なら早稲田！というわけでコマ大チームは早稲田大学に向かった。学生にお願いして問題を解いてもらった。早くも正解を出したが、今回は速さで勝負。もっと早く解ける人はいないかと探し求めたところたどり着いたのは「バンザイ同盟」お祝い事などで盛大にバンザイで演出をするというサークル。

大学もこんなサークルよく認めているな

　バスケットで早稲田と対戦するとこてんぱんに負けてしまうバスケ部所属の東大生伊藤さん。しかし頭脳じゃ負けない、といわんばかりに問題は特につまるところもなく解いてしまった。しかし間違いに気が付き再度計算をやり直す。一方大学時代、早稲田は「田舎くさい」イメージを持っていたマス北野、こちらもちょっと悩んだがどうにか解き終えた模様。２組とも６分３０秒ほどかかったがわずかの差で東大生が早かった。

コマ大チーム	９６０
東大生チーム
マス北野

正解…９６０、全員正解！

自然数を素因数分解する。例えば９０を素因数分解すると ９０＝２×３＾２×５（＝２＾１×３＾２×５＾１） 　９０の約数は９０つまり「２×３＾２×５」を割り切ることができるため各約数は ２＾ｘ×３＾ｙ×５＾ｚ という形をしている。割り算をすると 　９０／（２＾ｘ×３＾ｙ×５＾ｚ） ＝（２＾１×３＾２×５＾１）／（２＾ｘ×３＾ｙ×５＾ｚ） ＝２＾（１−ｘ）×３＾（２−ｙ）×５＾（１−ｚ） となる。 約数「２＾ｘ×３＾ｙ×５＾ｚ」と割った答え「２＾（１−ｘ）×３＾（２−ｙ）×５＾（１−ｚ）」はともに自然数でなければいけないため ０≦ｘ，０≦ｙ，０≦ｚ ０≦１−ｘ，０≦２−ｙ，０≦１−ｚ これより「０≦ｘ≦１，０≦ｙ≦２，０≦ｚ≦１」 となるため９０の約数の数は 　（ｘの２通り）×（ｙの３通り）×（ｚの２通り） ＝２×３×２＝１２個 この「１，２，１」は９０を素因数分解したときのそれぞれ２，３，５のべきの値。 一般に、自然数を素因数分解して Ｐ＾ａ×Ｑ＾ｂ×Ｒ＾ｃ×…（Ｐ，Ｑ，Ｒは素数） という形のとき、この自然数の約数の個数は （ａ＋１）（ｂ＋１）（ｃ＋１）… となります。

問題は「約数の個数が２８個」の自然数を求めるため、 （ａ＋１）（ｂ＋１）（ｃ＋１）…＝２８ となるａ、ｂ、ｃ…を求めます。ａ、ｂ、ｃ…は１以上の数のため上の積の括弧の数は２以上でなければいけません。そうすると括弧の数は多くても２×２×７＝２８の３個までになります。 左辺の積が括弧１個だけのとき「ａ＝２７」となります。様々な可能性がありますが、元の自然数が小さくなるのは ２＾２７＝１３４２１７７２８ のとき。 左辺の積が括弧２個のとき「ａ＝１、ｂ＝１３」「ａ＝６、ｃ＝３」…など様々な可能性がありますが、この中で元の自然数が小さくなるのは ２＾６×３＾３＝１７２８ のとき。 左辺の積が括弧３個のときは「ａ＝６、ｂ＝１、ｃ＝１」となる。同様に様々な可能性から元の自然数が小さくなるものを求めると ２＾６×３＾１×５＾１＝９６０ のとき。 この値が全体の中で最小の自然数となる。実際に約数を調べると 1 2 4 8 16 32 64 3 6 12 24 48 96 192 5 10 20 40 80 160 320 15 30 60 120 240 480 960 と２８個あることが確かめられる。

もう少し骨のある問題が欲しいな…

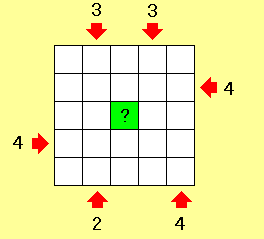問題：ある区画に２５個のビルが５行５列の正方形状に並んで建っています。 右の図は真上から見たビルを表しています。 １．ビルは１〜５階建てのいずれか。 ２．同じ行、同じ列でビルの階数は全て異なる。 ３．矢印の数字はその方向から見えるビルの個数。 以上の条件を満たすとき、中央のマス目のビルは何階でしょう？

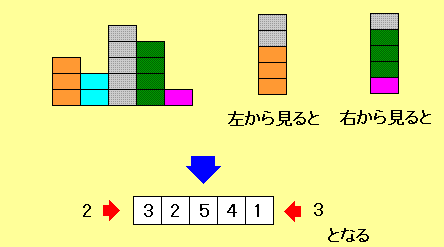
ビルの並びと数字の関係： 左から「３階、２階、５階、４階、１階」のビルが並んでいるとき この列の左から見ると３階と５階の２つのビルが見える （間の２階のビルは見えない） 反対に右から見ると１階、４階と５階の３つのビルが見える。

こんな簡単な問題出されちゃ…

　先週に続きダンカン部長はテレビドラマの監督兼弁当配りのためスタジオはお休み。検証のみの出演だった。「ビル」の問題なら「ビール」？？？というわけで？？？ビールの缶をテーブルの上に問題の条件を満たすように積み上げていく。途中で積み上げたビールが倒れたりしたが、意外や意外の秒殺か…と思ったところで間違いを発見。
　仕方なく一から積み上げ直すことに…秒殺の夢はまたの機会、というわけで３時間かけて答えを導いた。

　コマ大の検証を見ながらも私は問題の数字を入れていき、答えを導いた。答えの中央のマス目のビルは「２階」さあ、後はゆっくり見ようかな…と思ったところでふと考えた。

どうやって解いたっけ…

　東大生のプチ情報は「最近スカウトされた話」オフィス北野の人から「コマ大に出演しませんか」とスカウトされた小橋さん。一方振り返った途端にスカウトが断ってしまった岡本さん。嬉しいような少々腹が立つようなお話が二つありました。

　解答は次の通りになりました。

コマ大チーム	２階	検証の結果
東大生チーム	２階	５階のビルの位置から決めていった
マス北野	「に」階？？ （１に線を書き加えた）	東大生と同じく５階のビルの 位置は分かったがその後で 分からなくなった

正解…２階、コマ大、東大生チーム正解

　では解説です。

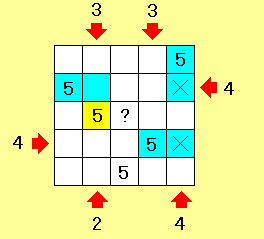
まず５階のビルの位置を決める。例えば矢印の数字が「４」のとき、５階のビルは必ず矢印の位置から４番目より向こうになければいけない。ということは問題の３つの矢印の「４」というヒントから青のマス目に５階のビルがある可能性がある。 　しかし「同じ列に同じ階のビルがない」という条件から、×印のマス目に５階のビルはない。このことから右２列の５階のビルの場所がわかる（左側の青のマス目はまだ） 　また左から２列目の上の矢印に「３」下の矢印に「２」の条件とすでに入った５階のビルから黄色のマスに「５」が入り、残りの５階のビルの位置も分かる。

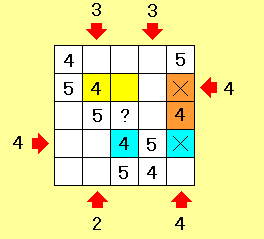
同じように４階のビルについても上から２列目の矢印から黄色の２マス、上から４列目の矢印から青色の２マス、一番右の列の矢印からオレンジ色の２マスのうち１つに４階のビルが入る。 　「同じ列に同じ階のビルがない」という条件から右の図のように４階のビルの位置が分かり、残り２つの４階のビルの場所も分かる。

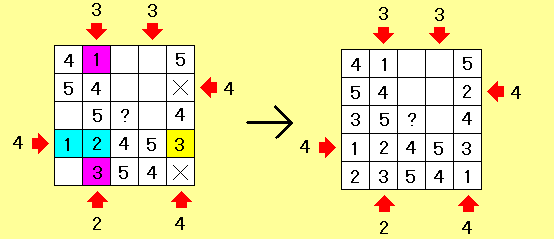
（左の図から）一番右の列で３階のビルが入るところを考えると×印のところは入れられないため、黄色の所に３階のビルが入る。そのあと矢印の数字に合わせるビルの並びを考えると青の二ヶ所のビルの階数が分かり、そのことから紫の二ヶ所のビルの階数も分かる。 　あとは「同じ列に同じ階のビルがない」という条件を使うと右の図のところまで分かる。

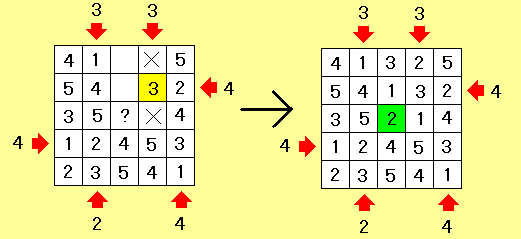
右から２列目の３階のビルが入る場所を考えると、上から３番目の列にすでに３階のビルが入っているため３番目はダメ。また上の矢印の数字が「３」であることから一番上もダメ。ということで上から２番目の場所に３階のビルが入る。 あとは「同じ列に同じ階のビルがない」という条件を使い「つつつーーっ（？）」とと解けます。 　これで中央のビルが「２階」であることが分かります。