「コマ大数学科」に挑む・10年11月
最終更新日2011年3月21日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「SUGA QUEST (10/13) おまけ」 |
| 「離散空間 (11/3)」 |
| 「パリティ (11/10)」 |
| 「ローリングトライアングル(11/17)」 |
| 「フェルミ推定(11/24)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「SUGA QUEST (10/13) おまけ」
第2のボスが出した問題。
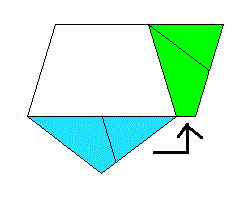
| 問題:正5角形をはさみで切って、正方形になるように並べ替えなさい。 |
|
ヒント3:図のように平行四辺形を作る。
|
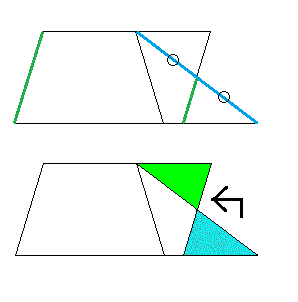
切り取り線の引き方: |
|
ヒント1:正方形は図の点線部が一辺になるように並べ替えられる。 ヒント2:まず対角線に沿って切る。
|
|
1:平行四辺形の高さと同じ一辺を持つ正方形を作り、1つの頂点は平行四辺形の 右下の頂点と合わせる。 2:平行四辺形の底辺と同じ直径の円を引く。 3:正方形と円の交点と平行四辺形の左下の頂点を結ぶと正方形の一辺(青の線)を引くことができる。 |
詳しいことはご自身で考えてください。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・10年11月
「離散空間(11/3)」
|
問題:辺の比が1:√3の長方形の格子がある。その頂点を適当に選び結んでできる
一番小さい正六角形と、その次に小さい正六角形の面積比を求めよ。
|
正六角形の凧をヒントに検証開始!紙の上に問題の通りの格子を竹ひごで作っていく。いつものように試行錯誤を繰り返して、一番小さい正六角形と、その次に小さい正六角形と思える形を見つけ答えを出した。そのあとは見つけた正六角形の形に紙を切り、見事に凧を作り上げた。一足お先にお正月気分のコマ大チームである。
この検証を見ながらも私は問題に挑んでいた。実は私もコマ大同様試行錯誤で答えを出そうとしていた。
|
外側の正六角形は一辺の長さが4。 |
|
2つの正六角形の格子のマスを計算すると
青の正六角形:格子6マス分 以上から面積比は6:18=1:3 |
テレビではマス・ポヌペアも東大生チームも問題の図に線を引いて考えていた。いち早く答えを出したのはマス・ポヌペア。相変わらずマスは図形に強い。解答は以下の通りになった。
| コマ大チーム | 1:3 | 検証の結果 検証で作った凧も披露 |
| マス・ポヌペア | 辺の長さが2倍の正六角形より 小さいものを探した結果 | |
| 東大生チーム | 格子点の間の距離を 求めて探した |
正解…もちろん 1:3、全員正解!!
ではどのようにして一番小さい正六角形と、その次に小さい正六角形を見つけるのでしょうか?
|
このうち「長さ2の線分」と「長さ2√3の線分」がそれぞれ120度の角度(図では60度の角度)をなすように線分を引くことができる。 つまり、この2本の線分で最も小さい正六角形と2番目に小さい正六角形を作ることができる。 |
結局は試行錯誤ということです。
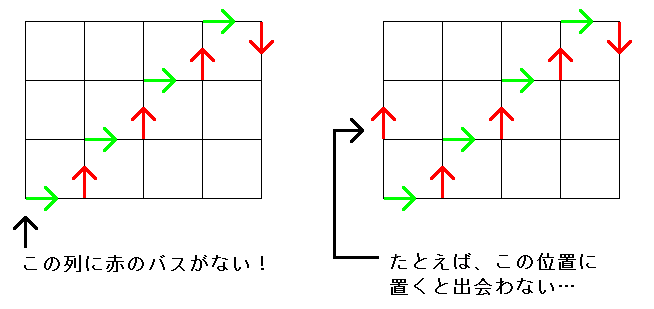
答えに出てきた2つの正六角形は辺のいずれかが格子の縦または横の線に沿ったものになっている。ではこの格子で作られる正六角形はすべて辺のいずれかが格子の縦または横の線に沿ったものになるか…というとそうではない。
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・10年11月
「パリティ(11/10)」
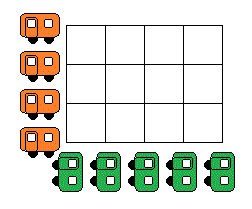 問題:縦に5列、横に4列の碁盤の目状になっている道の各行・列にバスを一台ずつ走らせる。
問題:縦に5列、横に4列の碁盤の目状になっている道の各行・列にバスを一台ずつ走らせる。バスは同じ速さで一つの行・列を往復する。 バスを交差点に配置した状態から走り始めて、バス同士が出会うことが無いようにするためにはどのように配置すればよいか? |
コマ大の検証はもちろんバスを使う。と言っても、紙工作で作って小さいバスを電車ごっこのようにして地面に引かれた線にそって問題の通りに動く。しかしコマ大チーム4人では足りないため、ゲストも登場。
私は検証を見ながらそそくさと答えを見つけてしまった。
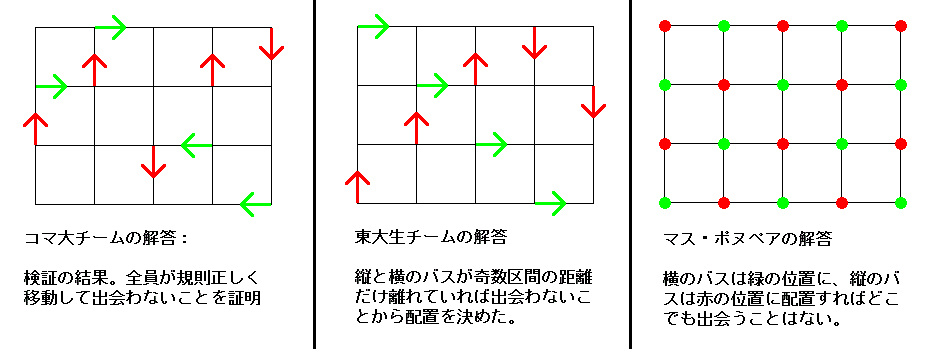
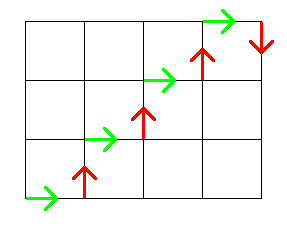 矢印のお尻の交差点にバスを配置して、矢印の方向に走らせるとバス同士出会うことはない。
矢印のお尻の交差点にバスを配置して、矢印の方向に走らせるとバス同士出会うことはない。走っているある時点で赤と緑のバスが隣の交差点の位置にある場合はバス同士出会うことはない。 |
|
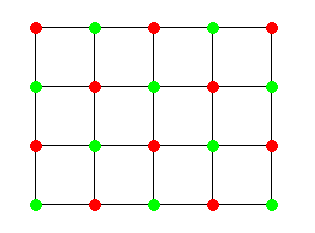 右の図のように互い違いに赤と緑の印をつける。バスは常に「赤⇒緑⇒赤⇒緑⇒…」と交互に交差点を通る。
右の図のように互い違いに赤と緑の印をつける。バスは常に「赤⇒緑⇒赤⇒緑⇒…」と交互に交差点を通る。赤と緑の交差点から走り始めるバスは、同じ時点では違う色の交差点にあるため、バス同士が出会うことはない。 つまり縦に走るバスは赤(または緑)の交差点、横に走るバスは緑(または赤)の交差点から走り始めるとバス同士は出会うことはない。 |
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・10年11月
「ローリングトライアングル (11/17)」
|
問題:原点が中心で半径1の円に内接する正三角形が原点を中心に回転するとき第1象限
にある部分(図の緑の部分)の面積の最大値と最小値を求めなさい。
|
コマ大ロケにノーギャラで来る「コマ女」を募集していたコマ大チーム。それでオバちゃんとか来たらどうするんでしょうか?そんなコマ大チームの挑戦は大きな正三角形のフェルト地を使って検証。回転する台の上に三角形を置き、最大・最小と思われるところを見つけてフェルト地を切り重さをはかる…それだけだと普通すぎるので、今回は日ごろお世話になっている吉田プロデューサーにプレゼント。 切ったフェルト地をプロデューサーの顔に貼り付けていく。
さすが吉田プロデューサーの顔というか頭は貼り付けやすいのか、思い思いのヘアスタイル(?)を作り上げる。何だかうれしそうな吉田プロデューサーの表情。一応答えは出した模様です。
私はいつものようにコマ大の検証を見ながら真剣に問題を解いていた。だって何だか解けそうだから…
|
(本当は正三角形が45度傾いた図を書けばよいが、作れなかったのでこの図で勘弁を) 正三角形の中心の線を引いたとき、半径1の円に内接しているため赤の線分の長さは1、青の線分の長さは1/2となる。 青の部分は直角二等辺三角形であるため、底辺と高さは右の図の通りになる。従って青の部分の面積は1/4となる。 |
|
|
| コマ大チーム | 最小:0.3 最大:0.45 | 検証の結果。フェルトの 重さから面積を出した。 |
| マス・ポヌペア | 最小:2/3 最大:2√6/3 | 形は私の解答と同じ 面積までは出し切れなかった |
| 東大生チーム | 最小:√3/6 最大:1/(1+√3) | 最大は私の解答と同じ 最小は問題の左図の形を計算 |
正解…最小:1/4、最大:(√3−1)/2
東大生は最大値が正解!
私は両方とも正解!
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・10年11月
「フェルミ推定(11/24)」 コマ大は今回で200回!! 問題がまだ出されていない… は?
| 問題:東京23区にはいくつの下水道のマンホールがあるか推定せよ。 |
着実にマンホールを数えるダンカン部長とアタル。そしてのんびりと過ごすアル北郷。一方、地域の半分を任せられたお宮の松。おまけにこの地域はマンホールの数が少ない。文句を言いながらもマンホール探しに駆け回った。四者四様の方法で数え、出した答えがこちら。
|
カウントしたマンホールの数:237個。 フジテレビのある港区はフジテレビを含め5社のテレビ局がある。 さらに23区であることからマンホールの総数は 237×5×23 = 27255個 |
マンホールの数…約48万個
コマ大チーム、見事に外れた。ちなみにこの場合一つの区には約21000個のマンホールがあります。今回のテーマ「フェルミ推定」とは一部の範囲の値から全体の総数の近似値を求める方法なのです…って、コマ大チームの例題では分かりにくいかもしれませんが。今回はこのような近似値を求める問題を200問用意。くじで選ばれた問題を3組が考えていきます。今回は適した計算方法をした組を竹内先生が判定するそうです。選ばれた問題はこちら!
|
問題:富士山を地上でどれくらい遠くから見ることができるでしょうか? ただし、地球は建物などがない球形であるとする。 |
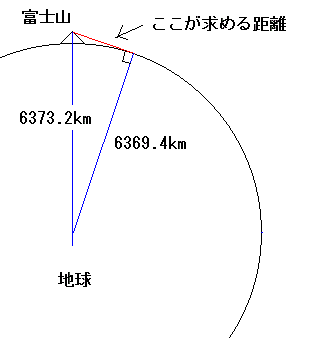 地球の中心、富士山の山頂、そして富士山が見える最も遠くの地点
の三点を結ぶと直角三角形ができる。
地球の中心、富士山の山頂、そして富士山が見える最も遠くの地点
の三点を結ぶと直角三角形ができる。地球の赤道一周は約4万kmであるため、地球の半径は 40000÷3.14÷2≒6369.4km この距離は地球の中心と最も遠くの地点の間の距離と同じである。 一方、地球の中心と富士山の山頂の間の距離は 6369.4+3.8=6373.2km である。このことから富士山から最も遠く見える地点までの距離は (6373.2)^2 - (6369.2)^2 ≒ 50970 ... |
| コマ大チーム | 1000km | 福岡県にある「富士見ホール」から見える、 と推測 |
| マス・ポヌペア | 1500km | 上の図の地球の中心での角度をもとに計算 |
| 東大生チーム | 514km | 計算は私の方法と同じ。富士山の高さを約4km 地球の半径を約6000kmとして計算 |
竹内先生は東大生チームの解答が適した計算と判定。東大生チームも途中で計算を間違えた模様である。計算をすると富士山が見えるもっとも遠いところの距離は約225kmとなる。
2問目はゲストを迎えて、ゲストに関する問題を出題。そのゲストは以前コマ大にも出演した林家ぺー・パー子夫妻。いつものように出てくるなり写真を撮りまくるお二人。テレビのカメラに見事に背を向けていた。ひとしきり撮り終えたところで問題!
| 問題:林家ペー・パー子夫妻が1か月で撮る写真の枚数を推定しなさい。 |
|
ペーさんは登場して5分ほどで20枚ほどシャッターを切っている。
その調子で1時間撮り続けると20×12=240枚になる。 1日10時間ほど撮っているとして、1か月30日、パー子さんと 2人が撮っているということから以下の計算となる。 240×10×30×2=144,000枚 |
多すぎるよな…
あくまで推定です。3組の解答も出た模様です。
| コマ大チーム | 24,000枚 | 1時間に400枚。1日に2時間撮り 1か月30日として計算 |
| 東大生チーム | 8.640枚 | 1時間に360枚。1日に8時間撮り 1か月15日仕事をし、2人分として計算 |
| マス・ポヌペア | 1,500枚 | 1か月15日写真を撮り、写真のチェックなど で1日100枚が限界として計算 |
実際に何枚撮っているのか、ペーさんによると「3,000枚」という解答。マスは一人分の枚数として計算した…みたい。
見てきたように「フェルミ推定」とは一部の範囲の値から全体の総数の近似値を求める方法です。 たとえば、ある神社の初詣の参拝客数を調べるとき、 一定時間に参道を通った人数を数え、そこから1日の参拝客数を求めるわけです。元々は原子構造などの物理の分野で考えられていた方法とのこと。原子という小さいものを調べる方法が大きいものを調べる方法に使われるとは不思議な感じがします。
今回はペーさんの写真の枚数の推理力が勝り、マス・ポヌペアにコマ大フィールズ賞が渡った。てんやわんやで200回。マスの数学への飽くなき挑戦はまだ続くようです。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・10年11月