「コマ大数学科」に挑む・11年1・2月
最終更新日2011年5月11日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「大阪大学に挑戦(1/26)」 | |||||
| 「2011年2月コマ大ダイジェスト(2/2〜2/9)」 | |||||
| 「2011年2月コマ大ダイジェスト後半(2/16〜2/23)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「大阪大学に挑戦 (1/26)」
|
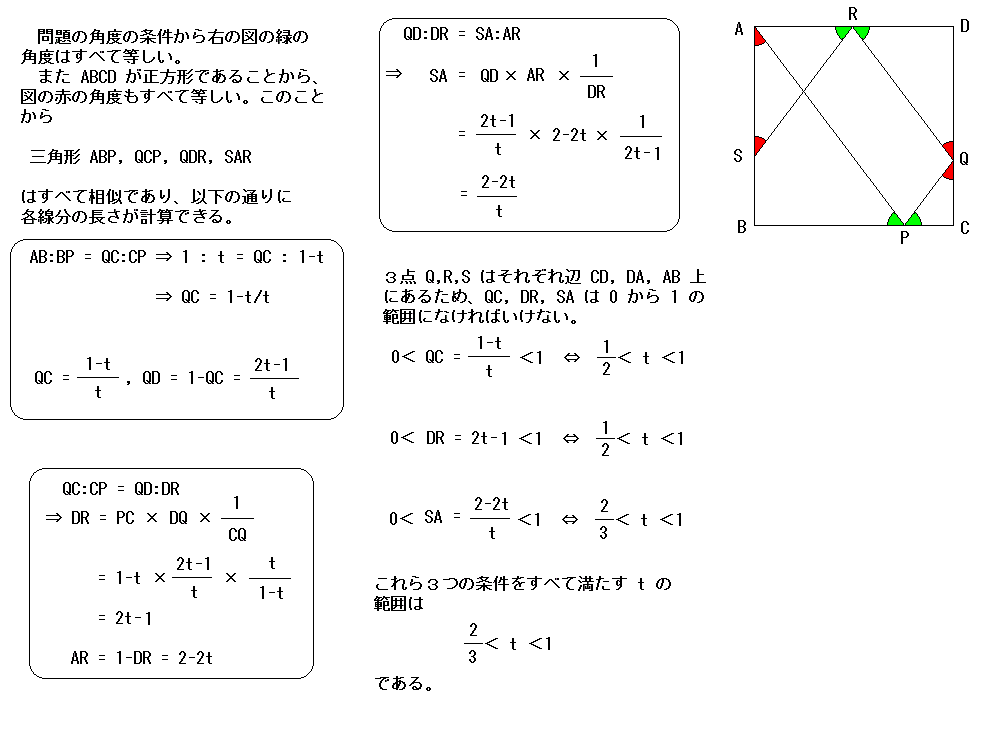
問題:1辺の長さが1の正方形 ABCD の辺 BC, CD, DA, AB 上に
点 P, Q, R, S を
∠ APB = ∠ QPC, ∠ PQC = ∠ RQD, ∠ QRD = ∠ SRA となるようにとる。BP の長さ t のとり得る値の範囲を求めよ。 |
スタジオでは着々と計算を進める東大生チームと図を書いて長い直線を引くマス。答えは、 そして時間はどうなるか?
| コマ大チーム | 2/3 < t < 1 | OBの解答。 |
| マス・ポヌペア | 3/4 < t < 1 | 以前のビリヤードの問題のように 解こうとしたが… |
| 東大生チーム | 2/3 < t < 1 | 正方形の頂点と P, Q, R, S との 長さを計算して求めた。 |
正解…2/3 < t < 1 コマ大チーム、東大生チーム正解!!
さて、阪大OBの社長と東大生チーム、どちらが早く答えを出すことができたでしょうか?
阪大OB…6分32秒 東大生チーム…8分45秒
わずかの差で社長が先に答えを見つけ出した。中村先生いわく「不本意ながら」コマ大チームにコマ大フィールズ賞が渡った。東大生チームが考えていた解き方は以下の通り。
|
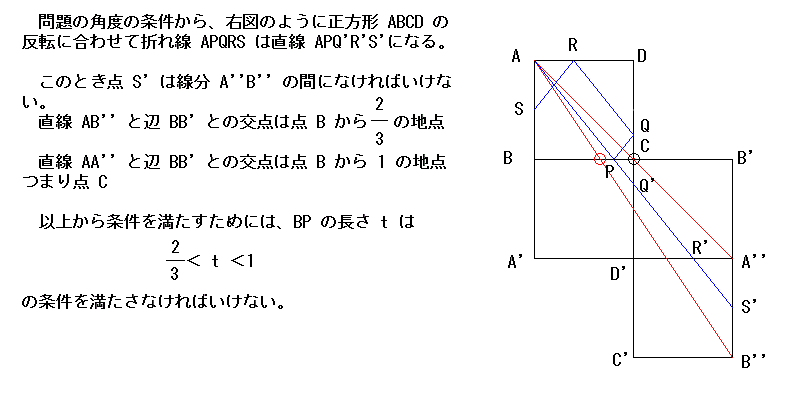
東大生の解答
|
|
私が考えた解答(中村先生の解説でも紹介)
|
「「2011年2月コマ大ダイジェスト前半(2/2〜2/9)」
「双六 (2/2)」 この回では東大生チーム・山田さんに代わって地デジカが登場。東大生チームの貴重な戦力に なったのでしょうか?
問題:さいころの目が丁度でないと上がれない双六をしています。
以下のうち、後戻りせずに上がれる確率が最も高いものはどれでしょう。
|
地デジカはやっぱり戦力にはならず、おまけに弁当まで注文。木村さん一人で問題に挑む。マス北野は「フィボナッチのように計算する」と話して計算を進めた。
| コマ大チーム | 2. ゴールの5マス手前 | 検証の結果。
4人中2人が 5マス前から上がった。 |
| マス・ポヌペア | 3. ゴールの7マス手前 | 上がるまでの目の 出方を調べた。 |
| 東大生チーム | 3. ゴールの7マス手前 | 漸化式を使って計算 |
正解…2. ゴールの5マス手前 コマ大チーム正解!!
コマ大チーム一人勝ちの番狂わせ。マスも木村さんも計算は正しかったが、7マス手前になると確率の出し方がちょっと違う。 コマ大フィールズ賞は正解を出しちゃったコマ大チームに渡った。解説は以下の通り。
 |
「チャンパーノウン数 (2/9)」 謎多し「チャンパーノウン数」とは何なのでしょう。解説は後ほどにして問題。
|
問題:すべての自然数を順番につなげて書いていくとき、1万個目に書かれる
数字はいくつでしょう。
1,2,3,…と順番に書いていく。9までは一桁の数であるが、次の 10から2桁になるため、10個目の数は「1」、11個目の数は「0」 になる。 |
ここで登城したのが久々の「秒殺」東大生チームの衛藤・伊藤ペアが答えを早々と書き、 検算を行った。マスも計算方法を考え付いていた模様でコツコツと計算をして答えを出した。
| コマ大チーム | 7 | 検証の結果 |
| マス・ポヌペア | 7 | 計算の結果 |
| 東大生チーム | 7 | 計算の結果 |
|
各桁の数字をすべて書くと何個の数字が使われるかを計算する。
1桁 : 1〜 9 の 9個の数があるため、使われる数字は 9個 1万個目の数字まで残りは7111個。これらを1000、1001、…と4桁の数字を 書いていくときに7111個目の数字がどの数字の何桁目の数字になるかを考える。 7111÷4=1777 あまり 3 であるため、1万個目の数字は「1000」から数えて1778個目の数の上から3桁目 (10の位)になる。「1000」から数えて1778個目の数は2777であるため、 1万個目の数字は7である。 |
今回のテーマの「チャンパーノウン数」とは 0.12345678910111213… と単に小数点以下に自然数を順番に並べただけの数。こんな誰でも思いつく数でも数学では大事な数になる、とのこと。私も正解を出しましたが、どの数字の何桁目の数字を調べるときに2777か2776かで悩みました。
「2011年2月コマ大ダイジェスト後半(2/16〜2/23)」
問題:直径がそれぞれ6cm、8cm、10cmのパイを1枚だけ切らずに
4等分する方法を作図で示しなさい。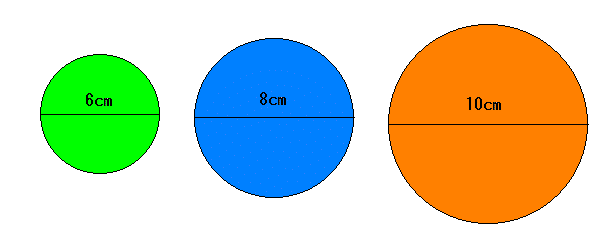
|
マスは久々のひらめきで「秒殺」解答。一方東大生チームは計算で答えを出そうとするが作図の方法まで見つからない様子。以下のような解答となった。
 |
 |
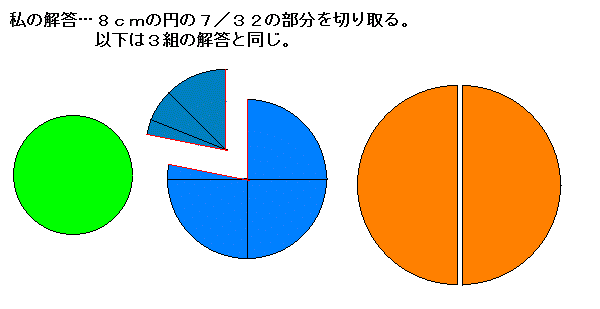
8cmの円の面積=16πより (7/32)×16π=(7/2)π
6cmの円と8cmの円の一部の面積: 9π + (7/2)π = (25/2)π となり、3つの円が4等分されたことが分かる。 |
「バレンタイン (2/23)」 2月といえば「バレンタイン」ということでこんな問題が出題された。しかし「いわくつきの問題」とのこと。
|
問題:人口1000人の村に1000軒の家があり、みんな一人で住んでいます。 バレンタインデーには自分の家から一番近い距離にある家に一個だけチョコをあげます。 家同士の距離はみな違い、村の外からチョコは届きません。 一人で最高何個チョコがもらえますか? |
スタジオでもマグロチョコが登場。その効果なのか、東大生チームは秒殺で解答。一方マスは「これでいけるんじゃないか」とこちらも早々と解答。
| コマ大チーム | 5個 | 検証の結果。
「東西南北の隣の家」と 「上の階の家」からチョコをもらう。 |
| マス・ポヌペア | 999個 |
ものすごく大きな家が一軒 あると考えた。 |
| 東大生チーム | 5個 | 6個だと不可能であることを 証明した。 |
正解…5個、しかし999個も正解!
「いわくつき」の理由はこの「999個」にあった。では解説。
模範解答
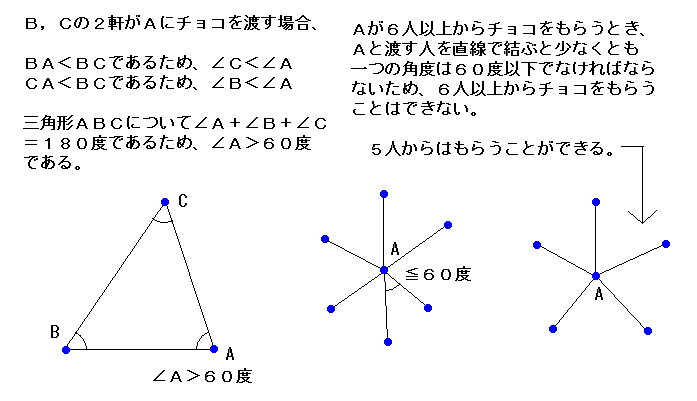 |
|
マス北野の解答(いわくつきの解答)
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年1・2月