「コマ大数学科」に挑む・11年3月
最終更新日2011年5月25日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「2011年3月コマ大ダイジェスト前半(3/2〜3/9)」 | |||||
| 「2011年3月コマ大ダイジェスト後半(3/16〜3/30)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「2011年3月コマ大ダイジェスト前半(3/2〜3/9)」
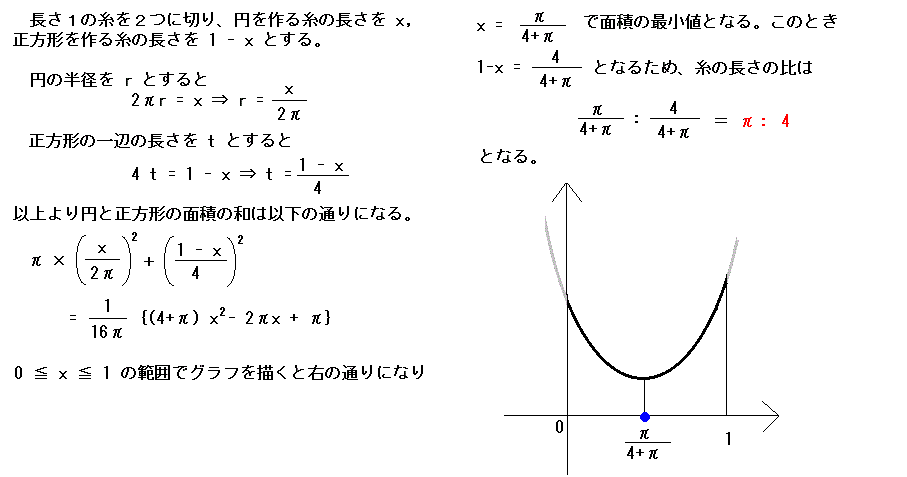
| 問題:長さ1の一本の糸を2つに切って、円と正方形を作る。このとき円と正方形の面積の 和が最小となるの2本の糸の長さの比を求めなさい。 |
| コマ大チーム | 円:正方形=8:17 | 検証の結果。 |
| マス・ポヌペア | 円:正方形=π/4:1 |
面積の和を式で表して 最小値を計算 |
| 東大生チーム | 円:正方形=π:4 | 面積の和を式で表して 最小値を計算 |
正解…円:正方形=π:4 東大生、マスチーム正解!!
今回の問題はコツコツと計算をしなければいけないようです。
 |
「回文数(3/9)」 「回文数」とは 101 や 24642 のように逆から書いても変わらない数のこと。で、問題。
|
問題:2ケタの数を逆に書いた数とその数自身を足していく。この計算を繰り返し、
回文数になるまで続ける。回文数になるまでの回数が最も多い2ケタの数を求めなさい。 ( 11 のようにすでに回文数になっている2ケタの数も少なくとも一回は計算をする) |
東大生チームもマス・ポヌペアもひたすら計算をしていく。足し算の筆算が三角形のように広がっていった。
| コマ大チーム | 99 | 検証の結果。 6回で終了。 |
| マス・ポヌペア | 89、98 |
繰り上がりが多いと思う 数から計算。 |
| 東大生チーム | 89、98 | 10の位と1の位の和で 場合分けして調べた。 |
正解…89、98 東大生、マスチーム正解!!
マスは最初に「89」を思いつき、計算が終わらないうちに時間が来た様子である。東大生チームのように場合分けをすると正解を導くことができる。
|
10の位と1の位の和を考える。
和が9以下である時、1回の計算で回文数になる。
和が10、12、13である時、2回の計算で回文数になる。
和が11である時、1回の計算で回文数になる。
(以下計算結果のみ表示)
和が15である時、4回の計算で回文数になる。
和が16、18である時、6回の計算で回文数になる。 |
|
98 → 187 → 968 → 1837 → 9218 → 17347 → 91718 → 173437 → 907808 → 1716517 → 8872688 → 17735476 → 85189247 → 159487405 → 664272356 → 1317544822 → 3602001953 → 7193004016 → 13297007933 → 47267087164 → 93445163438 → 176881317877 → 955594506548 → 1801200002107 → 8813200023188 |
「2011年3月コマ大ダイジェスト後半(3/16〜3/30)」
「楕円 (3/16)」
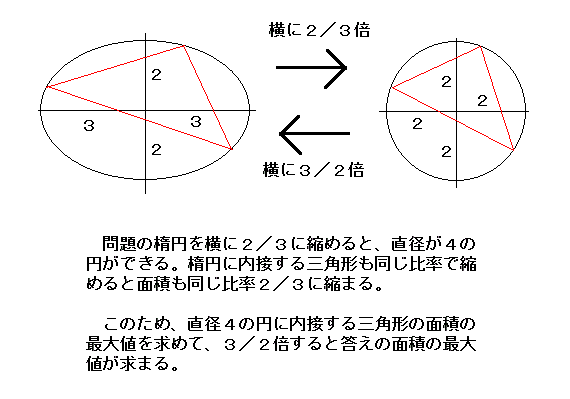
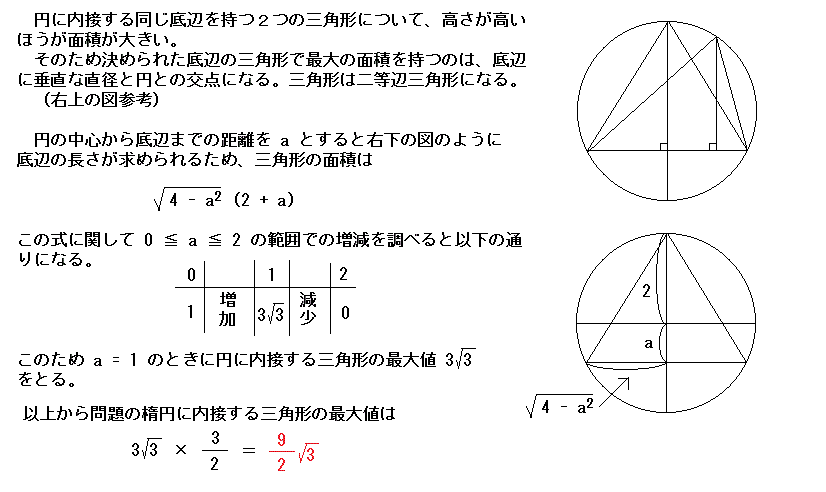
| 問題:長径が6、短径が4の楕円に内接する三角形の面積の最大値を求めなさい。 |
| コマ大チーム | 14g | アタルが円から正三角形を
切りだし、重さを量った。 |
| マス・ポヌペア | 9√3/2 |
円に内接する正三角形の 考え、それを横に伸ばした。 |
| 東大生チーム | 9√3/2 | 円に内接する正三角形の 考え、それを横に伸ばした。 |
正解…9√3/2 マス・ポヌペア、東大生チーム正解
見事に解法を見つけ出した2組。しかし「秒殺」を超えた「瞬殺」を見せた東大生チームにコマ大フィールズ賞が渡った。では解説。
 |
|
「箱 (3/23)」
|
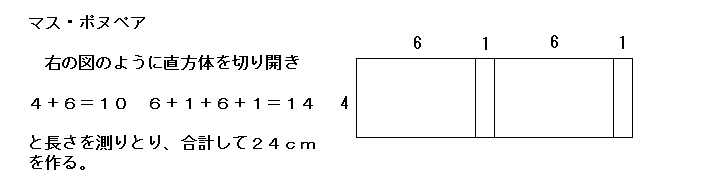
問題:縦4cm、横6cm、厚さ1cmの箱を使って長さ 24cmの長さを作図しなさい。 |
|
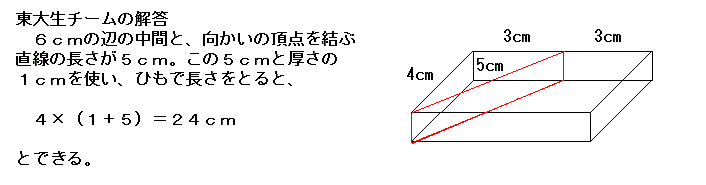
|
「卒業試験 Part2 (3/30)」
小橋・岡本ペアが晴れてコマ大を卒業。ということで今回は卒業試験。
問題:図のような鈍角三角形をなるべく少ない鋭角三角形で分割しなさい。
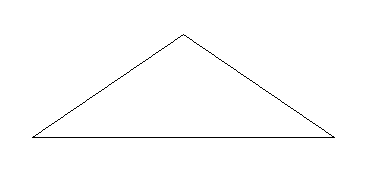 |
今回スタジオで問題に挑んだのはマス・ポヌペアと小橋さん一人。お互いに答えを出すことができました。
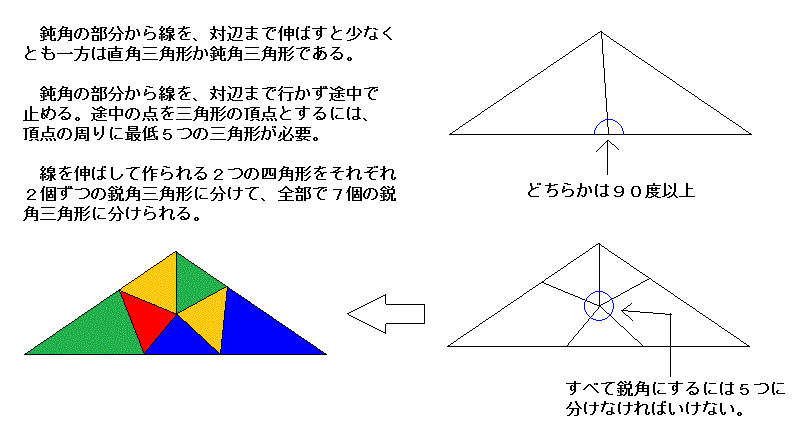
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年3月