問題は１０問。１問につき解答時間は３分。これが長いのか短いのか？まずは前半５問です。

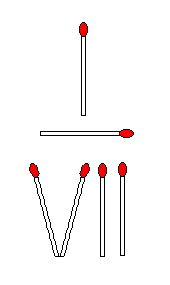
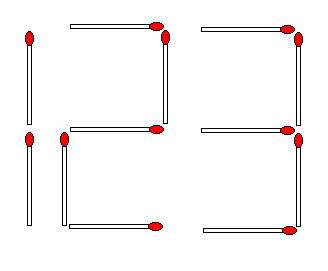
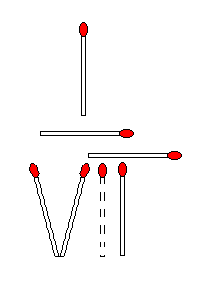
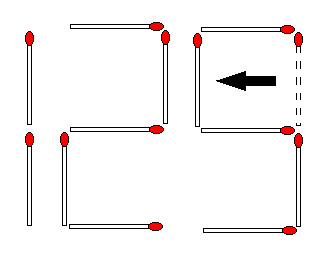
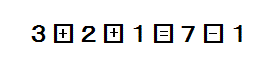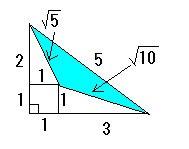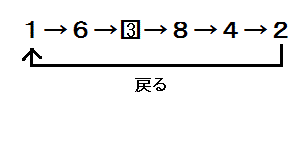
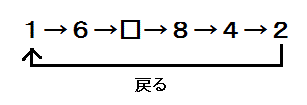
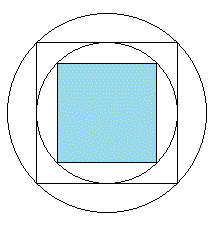
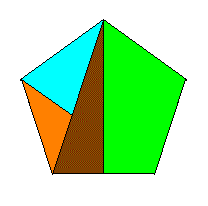
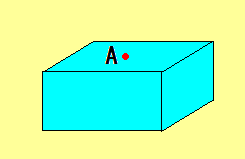
第１問： 下の四角の中に＋、−、＝ を入れて 等式が成り立つようにしなさい。 　ただし各記号は一個は使うこと。	第２問： 次の数列の規則を見つけ、 四角に入る数字を答えなさい。 タカさんからのヒント： 奇数と偶数に分けて考える。 ↑↑ドラッグしてください	第３問： ３つの正方形の土地に囲まれた池がある。 ３つの土地の面積が図の通りであるとき、 池の面積を求めなさい。
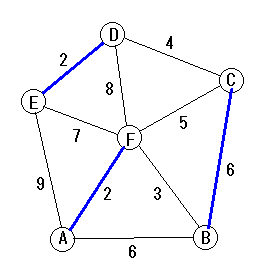
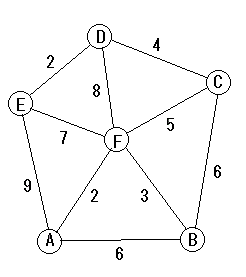
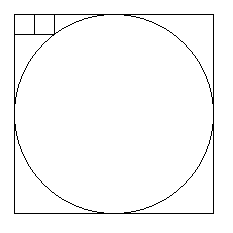
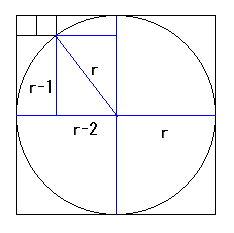
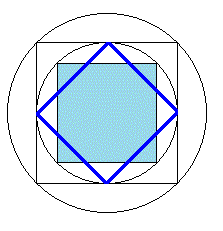
第４問 Ａ〜Ｆの町を結ぶ道路があり、距離は図の 通り。Ｆから出発しすべての道路を通りＦ に戻る経路を考えたとき、最短の経路の 距離を答えなさい。 　同じ道を何回通っても構いません。	第５問 ２個の小さな正方形が大きな正方形に接し、 右の正方形の一つの頂点が円周上にあります。 このとき大きな正方形の中に小さな正方形を 隙間なく敷き詰めるには何個必要か。

第６問： 図のように円と正方形が接しています。 外側の円の直径が１０ｃｍであるとき、 内側の小さい正方形の面積を求めなさい。	第７問： 図のように正五角形を分割して 並べ替えて、長方形にしなさい。
第８問：（放送で使われた図に重複した図がありました。勝手に図を変えました） 正方形６個をつないだ図形をヘキサミノといい、 回転や裏返しで一致する図形を同じものとみると ３５個あります。図に書かれていない３個のヘキサミノ を答えなさい。
第９問 図のようにマッチ棒が並べられています。 マッチ棒を一本だけ動かして１を表しなさい。 ただし、分数を表す横棒は動かしてはいけません。	第１０問 図のように並べられているマッチ棒を 一本だけ動かして、素数にしなさい。

「コマ大春の数学祭り(4/20) 解答」

第１問： ＝をどこに入れるかを考えると 答えは下の式になる。	第２問： 奇数であれば５を加える、 偶数であれば２で割る、という規則。 四角に入る数は３になる。	第３問： 池の３辺の長さは５、√５、√１０． 図のように直角三角形を作って考えると 池の面積は 3×4/2 - 1×2/2 - 1×3/2 - 1×1 　　　　　　　　　　　　　= 5/2
第４問 　すべての道を通るため、どの道を２回 以上通るかを考える。 　図の AF, BC, DE 間の道を２回通る 方法を考えると F, A, B, F, C, B, C, D, 　　　　　　　F, E, D, E, A, F とすべての道を通る方法が見つかる。 　このときの移動距離は６２となる。	第５問 　正方形の１辺の長さ１に対して円の 半径を r とする。このとき図のような 直角三角形ができる。 三平方の定理を使うと r = 5 であること が分かるため、正方形の面積は 100. つまり 正方形は 100 個敷き詰めることができる。

第６問： 　小さい正方形を図のように回転させると 大きい正方形の半分の大きさであること が分かる。 　大きい正方形の面積は 10×10/2 = 50 であるため、小さい正方形の面積は 25.	第７問： 　下の図の通り。茶色の三角形は裏返して並べる。	第８問： 下の３個。こつこつと調べると見つかります。
第９問 　図の通り。 分母が√１＝１となり、 １を表す式になる。	第１０問 　図の通りにマッチ棒を動かすと 「１２５」になるが、これを上下 逆にすると素数の「５２１」ができる。

正解数	称号	該当者
全問正解	数学の神	なし
８〜９問	数学の申し子	マス北野（８問）
５〜７問	ただの数学好き	瀬戸山さん、コマ大チーム、 竹内先生（５問）
２〜４問	下手の横好き	杉山さん、中村先生（４問） ＡＤ（３問）、ポヌさん（２問）
０〜１問	準レギュラー	なし

問題： 　３辺の長さが２０ｃｍ、３０ｃｍ、４０ｃｍの直方体があります。３０ｃｍ×４０ｃｍ面の中央の点Ａからの最短距離が最も長い面上の点を求めなさい。 　ただし、距離は表面上に沿って測るものとします。

コマ大チーム	50.6317 cm	真裏の中心点までの 距離を計測した。
マス・ポヌペア	10√29 cm	展開図を描き、点 A から 円を作り距離を調べた
東大生チーム		真裏の中心から ちょっとずれた所。 垂直２等分線を引いて 点を求めた

　正解は実際に箱に点をつけて紹介した。どのようにその点を決めたかをご紹介。