 問題:
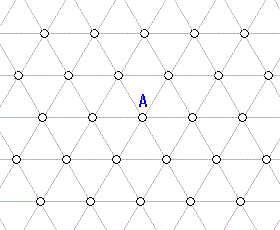
問題:1辺の長さが1の正三角形が敷き詰められた平面がある。頂点Aから出発して 三角形の辺上を1秒間に1動くとすると10以下で到達できる頂点の総数は 頂点Aを含めていくつあるか?
「コマ大数学科」に挑む・11年5月
最終更新日2011年7月1日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「除法 (5/4)」 | |||||
| 「福井大学に挑戦 (5/18)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「除法(5/4)」
|
問題: 5桁の数字が表示される電光掲示板があり、それぞれの桁には1〜7の どれかの数字が同じ確率で表示されます。 表示される5桁の数字が4で割り切れる確率を求めなさい。 |
東大生チーム、マス・ポヌペア共に計算方法が分かっていたようで早々と答えを書いてしまった。時間まで木村さんが撮った心霊?写真の話で盛り上がった。
| コマ大チーム | 11/50 | 100問の質問で 22問が4で割り切れた。 |
| マス・ポヌペア | 11/49 | 下2桁が4で割り切れるか 調べた。 |
| 東大生チーム | 11/49 | 下2桁が4で割り切れるか 調べた。 |
正解…11/49 マス・ポヌペア、東大生チーム正解!
コマ大チームの解答が非常に近かったのには驚いた。残り2チームの解説の通り、下2桁について調べればよい。
|
100=4×25であるため、100の倍数は常に4の倍数。
そのため3桁以上の整数について、下2桁の整数が4の倍数であればその整数は
4の倍数である。
例: このことから1〜7で作られる2桁の4の倍数の個数を求めれば5桁の4の倍数も 求めることができる。1〜7で作られる2桁の4の倍数は
12、16、24、32、36、44、 の11個。5桁の整数の上3桁は自由に数字を入れることができるため、 5桁の4の倍数の個数は7×7×7×11個。1〜7で作られる5桁の整数の 個数は7×7×7×7×7個であるため、5桁の4で割り切れる確率は
7×7×7×11/7×7×7×7×7 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年5月
「福井大学に挑戦(5/18)」
 問題:
問題:1辺の長さが1の正三角形が敷き詰められた平面がある。頂点Aから出発して 三角形の辺上を1秒間に1動くとすると10以下で到達できる頂点の総数は 頂点Aを含めていくつあるか? |
やっぱり
私も落ち着いて、落ち着いて秒殺でした。テレビではホームシックにかかった伊藤さん、寝込んだ時に集中して勉強ができた衛藤さんの話で盛り上がった。しかし、事件(?)はここから始まった。各組の解答は以下の通り
| コマ大チーム | 332個 | 花飾りを数えた結果 |
| マス・ポヌペア | 330個 | 点A以外の点を数えて 1個を加えた |
| 東大生チーム | 331個 | 6個の正三角形状の点の数 を数えて計算した。 |
正解…331個 東大生チーム正解!
コマ大チームもマスも途中で数え間違いがあった。ここでは東大生チームの計算方法と別の方法による計算方法をご紹介します。
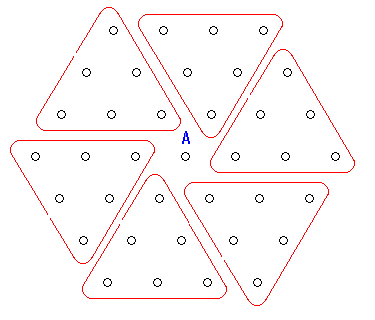 東大生チームの解答:
東大生チームの解答:例えば3秒以内に到達できる点は右の図の点である。 これを図のようにグループに分ける。そうすると点A以外は 6個の同じ大きさの正三角形の形に分けられる。この正三角形は 一辺に3個の点があるため、点Aを含めた点の総数は 6 × (3 × 4 / 2) + 1 = 37 個 この計算を10秒以内について同様に考えると点の総数は6 × (10 × 11 / 2) + 1 = 331 個 となる。 |
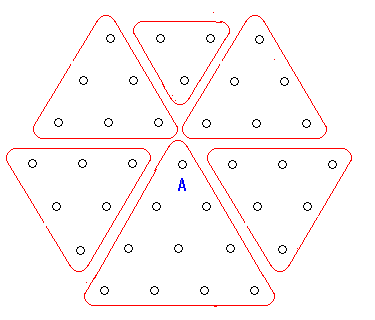 別の解き方:
別の解き方:同じ図を右のように6つの正三角形に分ける。三角形の 大きさは以下の通り
一辺に2個の点…1個、
一辺に3個の点…4個 以上から点の総数は
(2 × 3 / 2) + 4 × (3 × 4 / 2) + (4 × 5 / 2)
(9 × 10 / 2) + 4 × (10 × 11 / 2) |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年5月