 問題:
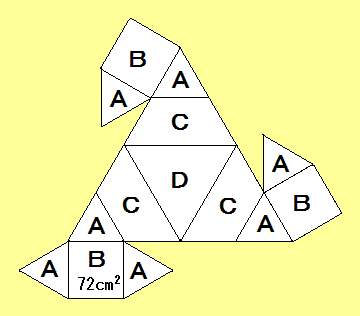
右の図はある立体の展開図です。
問題:
右の図はある立体の展開図です。
A:正三角形 B:正方形
A、Bの一辺の長さはともに等しい。
C:等脚台形 D:正三角形
CはAを3個つなげた形、Dの辺の長さはAの辺の長さの2倍。
Bの面積が72平方センチのとき、この立体の体積を求めなさい。
「コマ大数学科」に挑む・11年6月
最終更新日2011年8月10日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「展開図 Part 2 (6/1)」 | |||||
| 「反射 (6/8)」 | |||||
| 「必勝法 Part 6 (6/22)」 | |||||
| 「楕円 Part 2 (6/29)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「展開図 Part 2 (6/1)」
 問題:
右の図はある立体の展開図です。
問題:
右の図はある立体の展開図です。
A:正三角形 B:正方形
C:等脚台形 D:正三角形 Bの面積が72平方センチのとき、この立体の体積を求めなさい。 |
コマ大の検証で実際に作られる立体を見ることができたので、今回は早々と答えが出るかと思った。しかし、マスも東大生チームも展開図から立体を作り出した。そのあと立体を2つに切って…さてどうなったのでしょうか?
| コマ大チーム | 1820 立方センチ | 検証の結果 |
| マス・ポヌペア | 864 立方センチ | 2つに分けた一方が
正8面体の半分である。 |
| 東大生チーム | 一方は 1152 立方センチ もう一方は… | 2つに分けた一方が
正8面体の半分である。 |
正解… 1872 立方cm 全員不正解
今回も私正解を出しました。2組が行ったように立体を2つに分けて、それぞれの体積を求める方法もありますが、私はちょっと「ひねって」体積を求めました。
|
さらに三か所のBに四角すい(緑)を付けると右の図のように正八面体が作られる。このことから、求める体積は大きな正八面体から、付けた四角すいの体積3個分を引いたものになる。 |
|
まず、四角すいの体積から求める。四角すいの底面は正方形Bである。Bの面積は72平方センチである。Bの面積は (対角線の長さ)×(対角線の長さ)/2 で求めることができるため、対角線の長さは√(72×2) = 12センチ。このことから四角すいの高さが対角線の半分の長さ 6センチであることも分かる。以上から四角すいの体積は 正方形の面積×高さ/3=72×6/3=144立方センチ となる。
|
|
大きな正八面体の半分にあたる四角すいは、上で求めた四角すいと比較すると各辺の長さが2倍である。このため、正八面体の体積は上で求めた四角すいの2×2^3=16倍である。 求める立体は正八面体から四角すい3個分を除いた体積と等しいため、四角すいの16−3=13倍になる。よって体積は144×13=1872立方センチ |
「反射(6/8)」
学園祭シーズン、東大生・秒殺コンビは学園祭で骨密度や血圧を測っているそうです。
|
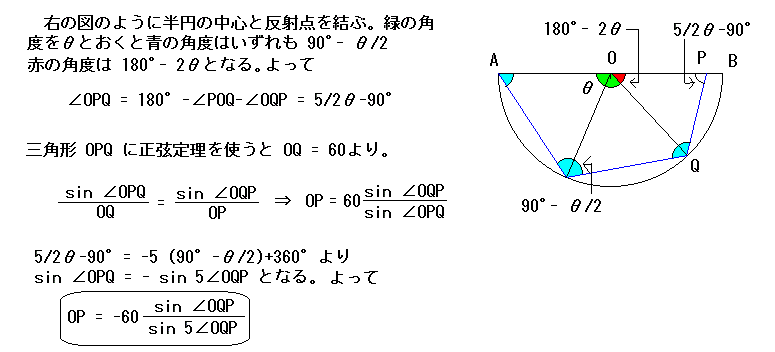
問題: AB = 120 を直径とする半円があり、A からの光が半円の内部で2回反射し、 OB 上の点 P を通るものとします。 光をいろいろな方向から出したとき、OP の最小値を求めなさい。
|
秒殺コンビは今回も秒殺、とまでは行かなかったが着実に計算を進め答えを出した。マスも分度器を使いながら図を書き答えを出した。
| コマ大チーム | 48.5 | 検証の結果 |
| マス・ポヌペア | 60 cos36° | 光が正五角形を 描くように進むと考えた。 |
| 東大生チーム | 60 cos36° | 光が正五角形を 描くように進むと考えた。 |
正解…48、全員不正解
最初この答えを見たときは「四捨五入して48」と思っていたが、そうではなく答えはちょうど48。 意外や意外の解説はこちら。
|

|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年6月
「必勝法 Part 6 (6/22)」
どうにかテレビ慣れした?東大生杉山・瀬戸山ペア。そろそろコンビ名が欲しいところ…と話したところで今回の問題。
|
問題: AくんとBくんが図のア〜ケ9つのマスに1,3,4〜10の数字を交互に一つずつ入れ ていく。
ルール このとき先手のAくんは、どのマス目にどの数字を入れると良いでしょうか。 |
|
「必勝法」シリーズに断然強いのはマス北野。しばらく考えて答えを早々と書いた。東大生チームも負けじと答えを出した模様。
| コマ大チーム | エまたはカに1を入れる | 検証の結果 アタルの結論 |
| マス・ポヌペア | エまたはカに1を入れる | 2が入る場合は 引き分けになることも解説 |
| 東大生チーム | エまたはカに1を入れる | 相手が最善手をとっても 勝てないことを解説 |
正解…エまたはカに1 全員正解!
では早速解説を
|
Aくんの点数とBくんの点数の差を求めると
(ア+イ+ウ+キ+ク+ケ)−(ア+エ+キ+ウ+カ+ケ) つまり「イ+ク」の和が「エ+カ」の和より大きいときにAくんの勝ちとなる。 |
|
Aくんが「エに1」を入れる ⇒Bくんは「エ+カ」の値を最大にするために、「カに10」を入れる。 ⇒Aくんは「イ+ク」の値を大きくするために、「イに9」を入れる。 クに入る数字は3以上であるため
(イ+ク)−(エ+カ) となるため、Aくんの勝ちが決まる。 マスに入る数字に「2」があるときは「クに2」を入れると引き分けにすることができる。 |
|
Aくんが他の数字の入れ方をした時を考える。
Aくんが「イ+ク」を大きくするために「イに10」を入れる
⇒Bくんは「カに9」を入れる。 となるため、Bくんの勝ちが決まる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年6月
「楕円 Part 2 (6/29)」
|
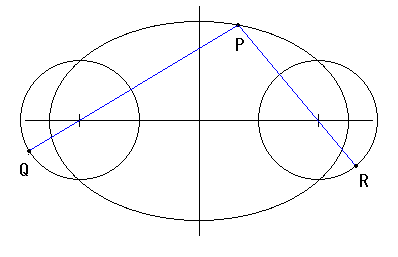
問題: 長軸の長さ10の楕円の2つの焦点を中心として半径2の円をかきます。 楕円上に点P,2つの円それぞれに点Q,Rを取るとき、線分PQ,PRの 長さの和PQ+PRの最大値を求めなさい。 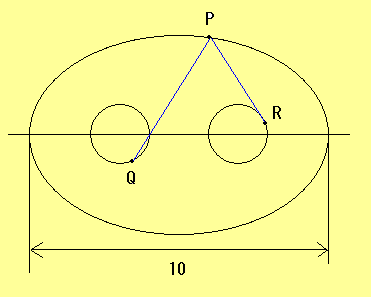
|
| コマ大チーム | 14.20 | 検証の結果 |
| マス・ポヌペア | 14 | 円上の点と焦点との距離の和が 一定であることから計算 |
| 東大生チーム | 14 | 円上の点と焦点との距離の和が 一定であることから計算 |
正解…14 マスチーム、東大生チーム正解!
あっさり解かれて中村先生がっくり。解説を加えることも無かったみたいです。
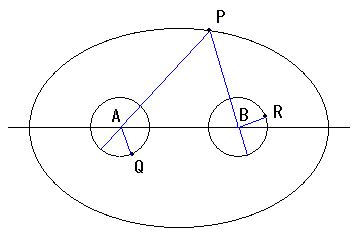
PQ ≦ PA + AQ, PR ≦ PB + BR PQ = PA + AQ となるときは点 Q は直線 PA と円 A の交点にあるときである。 点 R についても同様に考えるとPQ + PR ≦ (PA + AQ) + (PB + BR) = PA + PB + 4 A, B は楕円の焦点であるため PA + PB は P の位置にかかわらず長軸の長さ 10 と等しい。よって PQ + PR の最大値は 10 + 4 = 14 である。 |
こうなります。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年6月