数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１１年７月

「コマ大数学科」に挑む・１１年７月

最終更新日２０１１年８月２９日

フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。

「東北大学に挑戦(7/7)」
「切り口 (7/13)」
「共円 (7/20)」
「ピサの斜塔 (7/27)」

ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。

「東北大学に挑戦 (7/7)」

　おなじみ国立大学に挑戦シリーズ…とはいうもののコマ大メンバーはこれまで惨敗続き。そこで、コマ大スタッフもタッグを組んでＯＢに勝負に挑んだ。一番早く答えを導き出すのはどのチームか？

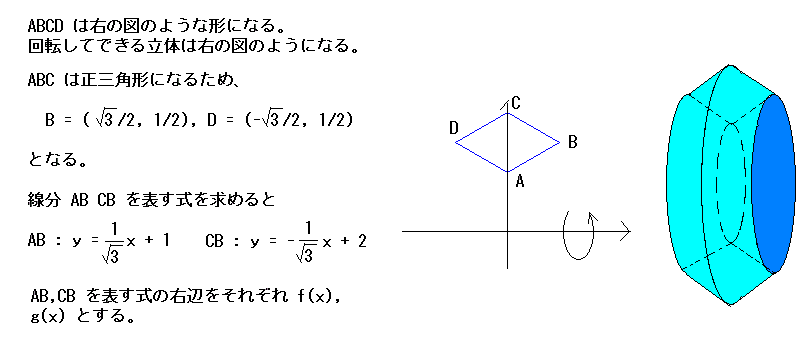
問題：
座標平面上に一辺の長さ１のひし形ＡＢＣＤがある。４点の条件は以下の通り

Ａ（０，１）　Ｃ（０．２）
Ｂは第１象限、Ｄは第２象限にある。

このひし形をｘ軸の回りに回転したときにできる立体の体積を求めなさい。

　東北大ＯＢとして登場したのは精神科医の徳永先生。いきなりコマ大チームのアラフォー４人衆の悩みを聞いたところで、問題に挑む。少し苦戦した（？）が正解を導いた。徳永さんいわく「竹内先生はこの解答を準備しているかも？」やはり敵は手ごわい様子。
　（今回の収録は３月の上旬。その後、東日本大震災により徳永先生も被災。しかし医師として他の被災者の支援にあたっていた。そのため今回の内容は数か月遅れの放送となりました。途中、お宮の松が問題を投稿する場面があったことを考えると３月頃であることがうなずける。）

　今回ＯＢに勝つべくスタッフが用意したのは東大生最強チーム（と勝手に命名）衛藤さん、マッハ伊藤さん、安川さんの３人。やはり同じ条件で問題に挑んだところ、一日の長か衛藤さんが一番早く答えを出した。
　今回スタジオの東大生チームは新入りの杉山・瀬戸山ペア。衛藤さんに勝てるのか？もしくは前回に続いてポヌさんが活躍するのか？解答は以下の通り

コマ大チーム？？？？徳永さんの解答は
後ほど
マス・ポヌペア３√３π／２積分を使って計算
計算はポヌさん担当
東大生チーム３π／２円錐の一部の体積
計算した。

正解…３√３π／２　マスチーム正解！

実は東大生チームも計算方法は正しかったが、計算をどこかで間違えてしまったみたい。円錐の体積を利用して正解を求めることもできたが、私も積分を使って答えを出した。

正解を出したのは徳永さん、衛藤さん、マス・ポヌペアの３組。一番早かったのはどのチームか？

徳永さん：６分３８秒衛藤さん：６分１４秒マス・ポヌペア：５分０秒

マス・ポヌペアの大勝利ということで文句なしのコマ大フィールズ賞！

数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１１年７月

「切り口 (7/13)」

　今回は名古屋大学が主催する数学コンテストで出題された問題

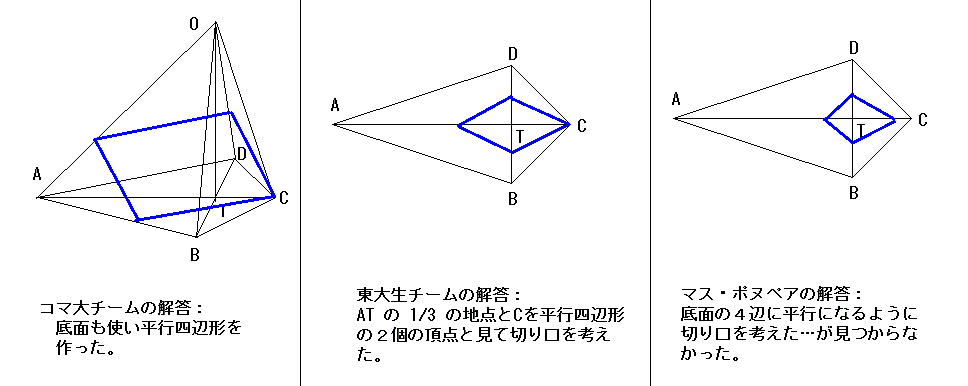
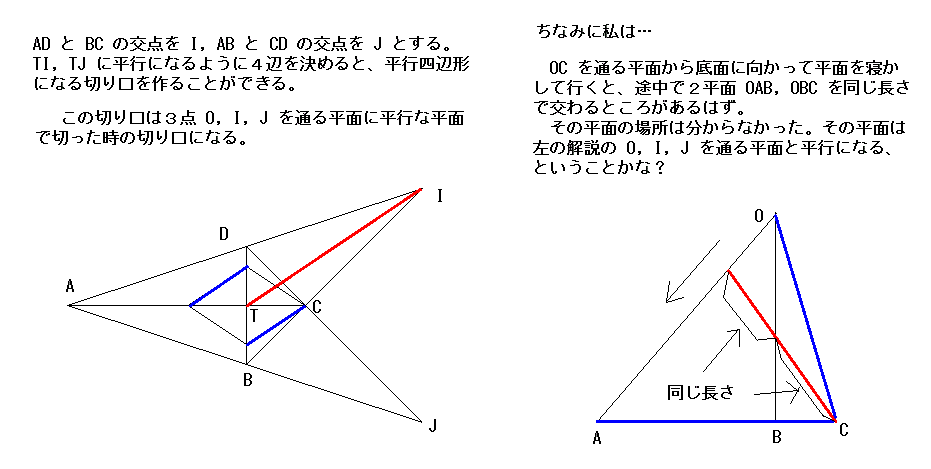
問題：
　下の図のような四角すいを平面によって切り、 切り口が平行四辺形になるとき、その切り方を作図しなさい。

コマ大チームの検証は実際に四角すいを切ってみよう…ということで向かったのは居合抜きの道場。ずっしりと重く切れ味鋭い真剣を持つとさすがにボケることもできなかった。少し手ほどきを受けたところで師範に問題の四角すいを切っていただくことに。師範も普段とは勝手が違ったがどうにか平行四辺形のような切り口を作ることができた。

中村先生の判定では東大生チームは正解。用意していた解答は以下のとおり。

マスは解説の図を書いていたが答えまではたどり着けなかった。コマ大フィールズ賞は東大生チーム。

数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１１年７月

「共円 (7/20)」

　今回は東京大学の学生が考えたゲーム「共円」に挑戦。と、その前にゲームのルールをご紹介。

共円のルール：

・２人（２組）で行うゲーム。
・正方形のマス目の書かれた盤面の線の交わるところにコマを 交互に置いていく。
・ある時点で４個のコマが同じ円周の上に置かれたとき、次に コマを置く人は「共円」と宣言し、４個のコマを指摘する。この 宣言が正しければ宣言した人の勝ち。
・４個のコマが一直線上に並んだ場合も「共円」と宣言しなければならない。

コマ大は手ほどきを受けにこのゲームを考え出した学生のもとを訪れた。始めはルールを理解することに一苦労だったコマ大チームだったが、次第にコツをつかみ「共円」の醍醐味を知ることとなった。そこで何を思いついたのか、とあるソフトウェアの会社に伺い、このゲームの売り込みを始めた。何が何だかわからないままコマ大のビデオは終了。

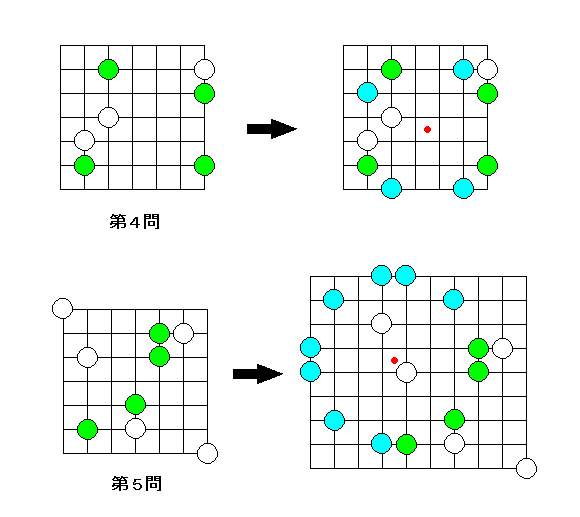
　今回は「共円」の中でも「詰め共円」を考えてみる。これはいくつかのコマが置かれている盤面を見て、同じ円周の上に置かれた（詰めになった状態の）４つのコマを見つける、というもの。

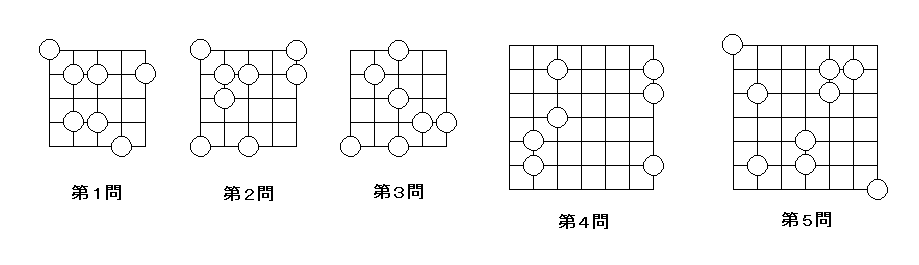
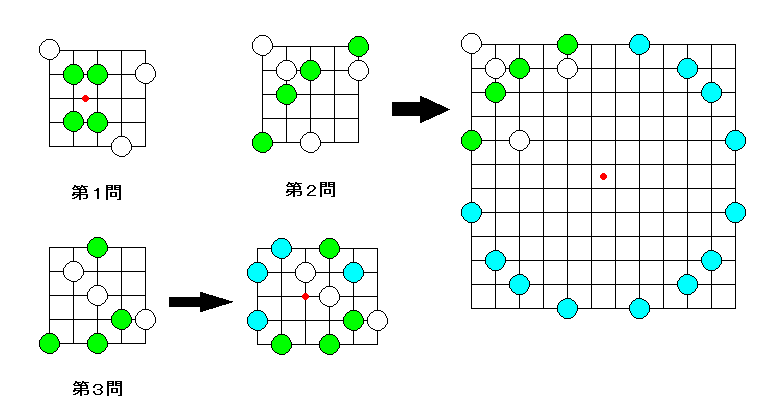
　私は１問目、２問目は分かったが３問目以降はさっぱりわからなかった。ゲームのコツをつかんだコマ大チームであったが、やっぱり（？）苦戦した。残り２組もやや苦戦した。 上の問題の解答は以下の通り。

それぞれ緑色の４個のコマが正解、赤の点が円の中心になる。

１問目は長方形をなす４個のコマを見つければよい。
２問目は等脚台形をなす４個のコマを見つければよい。大きい盤面で新たにコマ（水色のコマ）を置いていくと円をなすことが分かる。
３問目も４個コマを加えると８角形をなすことが分かる。

　結果はマス・ポヌペアと東大生チームが３問ずつ、コマ大チームは１問。最後の問題を１チームだけ答えた、ということでコマ大フィールズ賞はマス・ポヌペアになった。

数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１１年７月

「ピサの斜塔 (7/27)」

　ガリレオの落下に関する法則でおなじみのピサの斜塔の問題（というが、実際は落下の実験でピサの斜塔は使われていないとも言われている。ま、いいか）

問題：
ピサの斜塔から高さ１８０フィートの位置からボールを落とす。 ボールは地面にぶつかると落ちた高さの１／１０の高さまで跳ね返る。 このときボールが止まるまでのボールの移動距離の合計を求めなさい。

　コマ大チームは実際にボールを落として検証を行った。高さ１８ｍの地点からボールを落としていく。落ちた高さの１／１０の高さまで跳ね返るボールとしてスカッシュのボールを使いボールの移動距離を足していった。
　今回は解き方が分かっていたようで、東大生チームは早々と答えを出した。マスも一歩遅れたが答えを出した。

コマ大チーム220.4 フィート検証の結果
マス・ポヌペア220 フィート距離を足すと 219.9999...
となった。
東大生チーム220 フィート無限級数を使って計算

私うっかりミスをしておりました。単に「180 + 18 + 1.8 + ...」を計算するだけで、往復（跳ね返って戻るとき）の移動距離を考えていませんでした。

正解…220 フィート　マス・ポヌペア、東大生チーム正解！

　中村先生いわく「コマ大チームが正解に近い値を出したことに驚いた」とのこと。解説は以下のとおり。

　ボールが最初に地面についてから跳ね返るとき 180 フィートの 1/10 の 18 フィート跳ね返る。その後地面まで 18 フィート落ちるため、一回地面に着いてから次に地面につくまで 36 フィート移動する。
　同様にして次に地面につくまで 36 フィートの 1/10 の 3.6 フィート移動する。これを続けると 移動距離の合計は

　180 + 36 + 3.6 + 0.36 + ...
＝180 + 36 (1 + 1/10 + 1/10^2 + 1/10^3 + ...)

ここで 1 + 1/10 + 1/10^2 + 1/10^3 + ... がいくつになるか計算をする。

以上より移動距離の合計は

　180 + 36 × 10/9
＝180 + 40
＝220 フィート

コマ大チームの結果に驚いてはいたが、コマ大フィールズ賞はやっぱり速かった東大生チームに渡った。

数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１１年７月