図のようにマス目に1、2、3…と順に数字を書き入れていくとき 1から右に10、下に10のマス目に入っている数字を求めなさい。
「コマ大数学科」に挑む・11年8月
最終更新日2011年10月14日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「生育条件 (8/3)」 | |||||
| 「コマ大ファンからの挑戦状 (8/10)」 | |||||
| 「階段 (8/17)」 | |||||
| 「ウラムの螺旋 (8/31)」 | |||||
| 「奇跡の軌跡 (8/31)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「生育条件 (8/3)」
|
問題: ある植物を以下の条件で栽培したとき、植物の成長は表の通りになった。
3条件の各要素には数字が与えられており、成長の長さは3条件の 合計で求めることができるものとする。 |
東大生チームは早々と答えを出そうとしたが、一応確認をして答えを出した。一方マス・ポヌペアはやたらと計算を進めた。ポヌさんは掛け算をし始めて…答えはでたのか?
| コマ大チーム | 「アルカリ」「長時間」「低温」で15cm | 検証の結果 |
| マス・ポヌペア | 「アルカリ」「長時間」「低温」で41cm | 計算をしていたが分からなく なった、とマス |
| 東大生チーム | 「アルカリ」「長時間」「低温」で34cm | 各要素の成長を式で表して計算 |
正解…「アルカリ」「長時間」「低温」で34cm 東大生チーム正解!
コマ大チームが成長は違えど条件が合っていたのには驚いた。マスも東大生も式を作って足して引いてを繰り返したが、もう少し簡単に計算ができる。
|
各条件の要素に対する成長の長さを以下のように変数をあてる。
x1 + y2 + z2 = 26
2(x1 + x2 + y1 + y2 + z1 + z2) = 88
|
||||||||||||||||||||||||||||||||||||||
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年8月
「コマ大ファンからの挑戦状 (8/10)」
以前マス北野が「小学校6年生の子供がやってきて『コマ大の問題を解いている』と話した」と 話していた。そんな小学生はいるのか?ということで、コマ大チームが探してみた。今回の問題は平方数・立方数を使った問題を3問。全員で協力して時間内に何問解けるかを競う。問題は以下の3問。
|
第1問: 3ケタ以上の平方数で10の位と1の位の和が偶数になるとき、1の位はいくつになるか。 |
|
第2問: 2以上の整数 m, n は m^3 + 1^3 = n^3 + 10^3 を満たす。m, n を求めよ。 |
|
第3問: How many numbers from 1 to 1 million, inclusive, are not perfect squares or perfect cubes? |
対するマス・ポヌ・東大生チームは各問題を分担して解いていく。ここで、いきなり答えを出したのはマス北野。第2問を手に取ると「あっ」という間に解いていしまった。マスと一緒に解く予定だったポヌさんは木村さんと一緒に第3問に挑む。山田さんは第1問。マスの勢いに乗ったのか2組とも解き終えた模様。
| 第1問:山田さんの解答 | 0または4 | 1の位の2乗を計算した。 |
| 第2問:マス北野の解答 | m = 12, n = 9 | ラマヌジャンの 逸話を思い出した。 |
| 第3問:木村さんの解答 | 998910個 | 詳しくは後ほど |
結果は…全問正解!
マス・ポヌ・東大生チーム見事に正解を導くことができた。第3問の問題の日本語訳と各問題の解説は以下の通り
|
第1問: 3ケタ以上の平方数であるため、この平方数は10以上の整数の2乗である。この整数を 10 a + b(a:正の整数、b:0以上9以下の整数)と表すと、 (10 a + b)^2 = 100 a^2 + 10 * (2*a*b) + b^2 となるため
(10 a + b)^2 の10の位= 2*a*b の1の位+ b^2 の10の位 ここで 2*a*b は偶数であるため1の位も偶数。よってこの平方数の10の位と1の 位の和が偶数であるとき b^2 の10の位と1の位の和も偶数である。 b が0以上9以下であるとき、b^2 の10の位と1の位の和が偶数であるものを 挙げると 0^2 = 00, 2^2 = 04, 8^2 = 64 の3通りのみである。以上からこの平方数の1の位は0または4である。 |
||||||||
|
第2問:
m^3 + 1^3 = n^3 + 10^3 → m^3 - n^3 = 10^3 - 1^3 = 999 つまりの立方数の差が 999 となる。m = 20 のとき、差が最も小さくなるときでも 20^3 - 19^3 = 1141 > 999 となるため、m は最大でも 19 でなければいけない。また m^3 と m, n^3 と n は3で割った余りが同じである。m^3 - n^3 は3の倍数であるため、 m - n も3の倍数でなければいけない。 m - n が3の倍数で、m^3 - n^3 の1の位が 9 になるものを挙げると、
|
||||||||
|
第3問:
How many numbers from 1 to 1 million, inclusive,
are not perfect squares or perfect cubes? 1,000,000 = 1,000^2 = 100^3 であるため、1 から 100 万の間に平方数は 1000 個、立方数は 100 個ある。 しかし、1 から 100 万の間には平方数でも立方数でもある数も含まれている。 平方数でも立方数でもある数とは整数の6乗で表される数のことである。1,000,000 = 10^6 であるため、整数の6乗で表される数は全部で 10 個ある。以上から平方数でも立方数でもない数 の個数は1000000 - 1000 - 100 + 10 = 998910 であることがわかる |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年8月
「階段 (8/17)」
暑い夏にはやっぱり怪談…ではなく階段の問題。
|
問題: 同じ強度の卵2個を使って15段の階段で落下テストを行い 卵の強度を測定する。卵2個が割れる前に卵の強度を測定できる方法を 考えたとき、最悪でも何回の落下テストをする必要があるでしょう。 (卵の強度はそれより上の段では割れてしまうギリギリのところで判定する) |
東大生チームは未だ「コンビ名募集中」の杉山・瀬戸山ペア。コマ大チームからの新コンビ名の案を無視し(?)問題に挑む。一方マスは何やらひらめいたよう。答えを書くのはタッチの差で東大生チームが速かった。
| コマ大チーム | 8回 | 真ん中(8段目)で1個卵を落とし、 上半分、下半分で下の段から調べる。 |
| マス・ポヌペア | 5回 | 下から5,4,3,2,1段に 分けて卵を落としていく。 |
| 東大生チーム | 9回 | コマ大チームと同じ調べ方 ただ、回数を数え間違えた。 |
正解…5回 マス・ポヌペア正解!
解説は以下の通り。
|
階段のある段から卵を落としたとき
卵が割れない
卵が割れた 例えば下から3段目では割れないが6段目で割れたとき、卵の強度は4,5,6段目の いずれかである。4段目から順に残り1個の卵を落として割れたところがその卵の 強度と判定できる。 |
|
2個の卵を k 回落として強度を測定できる段数を f(k) と表す。
最初に下から n 段目の所から卵を落としてみる。
卵が割れた → 2個目で 1, 2, ..., n-1 段目を測定。
卵が割れない → n 段より上で卵を k-1 回落として強度を |
|
f(k) の条件式「f(k) = f(k-1) + k」と「f(1) = 1」であることから
f(k) = 1 + 2 + ... + k = k(k+1)/2 となる。f(k) ≧ 15 となる k を求めると k ≧ 5 となり、最悪でも 5回の落下テストをする必要がある。実際に、1個目の卵を下から5、9、12、14、15段の順に 落としていくと5回以内に卵の強度を測定することができる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年8月
「ウラムの螺旋 (8/31)」
|
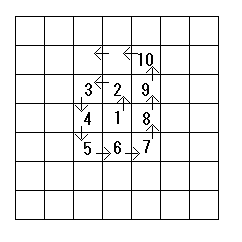
問題: 図のようにマス目に1、2、3…と順に数字を書き入れていくとき 1から右に10、下に10のマス目に入っている数字を求めなさい。
|
コマ大チームの地道な検証とは裏腹に東大生チームもマス・ポヌペアも早々と答えがでた模様。これは余裕かと思ったら、東大生チームが計算違いを見つけて修正。答えはどうなったか?
| コマ大チーム | 421 | 検証の結果 |
| マス・ポヌペア | 421 | 1の右側の数字を求めてから計算 |
| 東大生チーム | 421 | 1の右上の数字を求めてから計算 |
正解…421 全員正解!
タカさんが話したとおり、コマ大チーム向きの問題だったようでした。今回はポヌさんが1の右側の 数字を求めていったが、東大生チームの計算が少しは早いかもしれない。
|
1より右に 1、上に 1= 9=3^2 問題の「1より右に10、下に10のマス目」の数字は「1より右に10、上に10のマス目」の数字より20少ないため 441−20=421 となる。 一般に「1より右にN、下にNのマス目」の数字は 4N^2+2N+1 となる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年8月
「奇跡の軌跡 (8/31)」
|
問題: 図のように3つの車輪が取り付けられている観覧車がある。
中心の車輪Aは反時計回りで回転する。 観覧車の乗客が車輪Cに乗った時、通過する軌跡を描きなさい。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年8月