• 菊川怜さん…東京大学建築学科卒。インテリタレントの先駆け的存在。先日数学に関する本を出した。
• 葛西祐美さん…高校２年生。今年の中学女子数学オリンピックの金メダリスト。先日「数オリなでしこジャパン」の回にも出演（このとき「数オリ日本女子初の金メダリスト」と紹介しましたが、間違っていました。ごめんなさい）
• 黒田有彩さん…お茶の水女子大物理学科卒。現在グラビアタレントして活躍しているが、全国作文コンクールで入選をするなどの才女。「平成教育学院」などにも出演。
• 中島さち子さん…東京大学理学部数学科卒。河合塾の講師でありながらジャズピアニスト。国際数学オリンピックで日本女子初の金メダリスト（こちらは本当の事です）さらに葛西さんの指導をしていたこともある。

第１問：衛藤・伊藤ペアＶＳ中島・葛西ペアの問題 　ｎ！（ｎの階乗）の値の最後に０が１５個並ぶ、最小の整数ｎを求めなさい。

第２問：木村・山田ペアＶＳ菊川・黒田ペアの問題 　正三角形の土地を持っていた主人が妻と二人の息子に以下の遺言を残して他界した。 『長男は土地全体の２／３、次男と妻はそれぞれ土地全体の１／６をもらう。 ただし、いずれも同じ形に分けるものとする。』 正三角形の土地はどのように分ければよいでしょう。

第１問
中島・葛西ペア	６５	５の倍数を数えた
衛藤・伊藤ペア	６５	５の倍数を数えた
第２問
菊川・黒田ペア	解答見つからず。
木村・山田ペア	解答見つからず。

第１問…両者正解、第２問…両者不正解

第１問：「値の最後に０が１５個並ぶ」ということはその値は p × 10^15 = p × 2^15 × 5^15 という形で書くことができる。つまり n! の値の最後に０が１５個並ぶとき n! を素因数分解したときの５の指数は１５以上でなければいけない。 n! を素因数分解したときの５の指数は (n を 5 で割った商)＋(n を 5^2 で割った商)＋(n を 5^3 で割った商)＋… で計算できる。n = 64, 65 のとき上の式を使い計算すると 64 を 5 で割った商 = 12,　64 を 5^2 で割った商 = 2 65 を 5 で割った商 = 13,　65 を 5^2 で割った商 = 2 であるため、問題の条件を満たす整数 n は 65 である。

第２問：下の図の通り。緑が長男、赤と青が妻と二男の土地となる。

第３問：杉山・瀬戸山ペアＶＳ中島・葛西ペアの問題 　次の３つの図形 A, B, C の面積 Sa, Sb, Sc の大小関係を求めなさい。

第４問：マス・ポヌペアＶＳ菊川・黒田ペアの問題 　以下の表の空欄に数字を入れ、縦、横、対角線に並ぶ３つの数字の積が同じになるとき、x に入る 数字を答えなさい。

第３問
中島・葛西ペア	Sb ＜ Sc ＝ Sa
杉山・瀬戸山ペア	Sb ＜ Sc ＝ Sa
第４問
菊川・黒田ペア	512	２のべき乗の掛け算を考えた
マス・ポヌペア	512	２のべき乗の掛け算を考えた

第３問…両者正解、第４問…両者正解

第３問 以上から Sa = Sc が分かる。また π＞１であるため Sa ＞ Sb となり、３つの面積の大小関係は Sb ＜ Sc ＝ Sa となる。

第４問 　表の３つの数字が 2 の累乗であることに注目する。３個の 2 の累乗 2^a, 2^b, 2^c の積は 2^a × 2^b × 2^c = 2^(a + b + c) となる。問題の表のすべてに 2 の累乗を入れて縦、横、対角線に並ぶ３つの数字の積が同じになるとき 各数字の 2 の指数を考えると、縦、横、対角線に並ぶ３つの数字の和が同じになる。つまり指数は普通の魔方陣となる。そこで条件の数字の配置になる魔方陣を考えると以下の通りになる。 以上から x には 512 が入ることが分かる。ちなみにこのとき各列の数字の積は 2^15 = 32768 である。

問題： 　４桁の整数の中で、その整数の上２桁と下２桁を足して２乗するとその整数自身になるものを求めなさい。 　たとえば「１２３４」という整数の場合、上２桁「１２」と下二桁「３４」を足して２乗すると （１２＋３４）＾２　＝　４６＾２　＝　２１１６ となるため、１２３４とはならない。

　これといった解き方が見つからなかったマス、そして東大生チーム。ともに一つ一つ探してみることに、一方コマ大チームはスタジオでもかるたをとり続けた。

コマ大チーム	３０２５	見事に答えを探した
東大生チーム	２０２５、３０２５	場合分けをして考えた。
マス北野	３０２５、９８０１	しらみつぶしに探した。

正解…２０２５、３０２５、９８０１　全員正解！

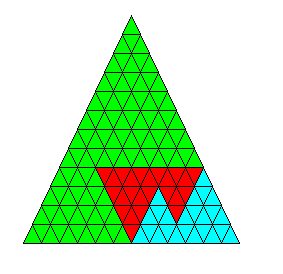
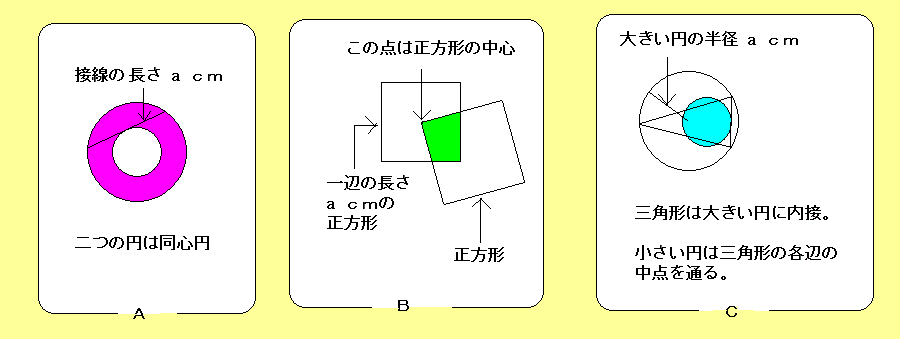
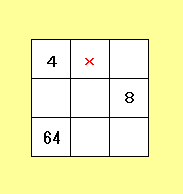
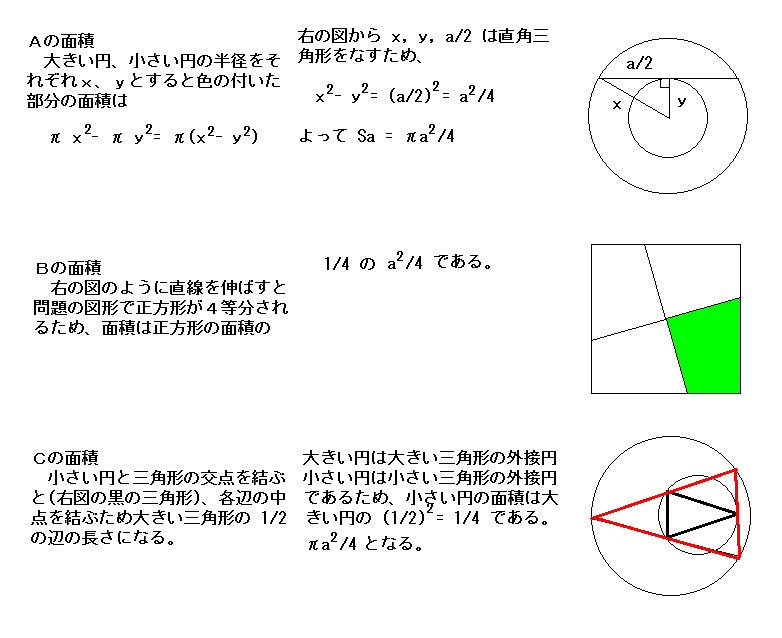
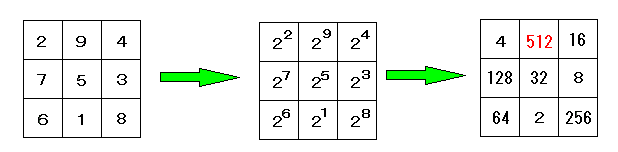
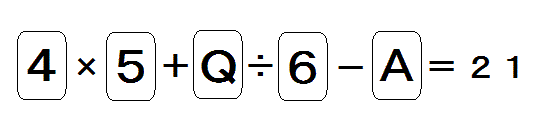４桁の整数の上２桁を x、下２桁を y と表すと、問題の条件は (x + y)^2 = 100 x + y となる。この式を展開して y でまとめると y^2 + (2 x - 1) y + x^2 - 100 x = 0 となる。この式を y の２次方程式と見たとき、整数の解を持たなければいけないため、 この２次方程式の判別式は整数の２乗である必要がある。 判別式 = (2 x - 1)^2 - 4 (x^2 - 100 x) 　　　 = 396 x + 1 この式が整数 n の２乗であるとき 396 x + 1 = n^2 ⇒ (n - 1)×(n + 1) = 396 x 　ここで n - 1, n + 1 は差が２の整数である。396 = 4 × 9 × 11 であるため、n - 1, n + 1 はともに偶数でなければいけない。 　さらに n - 1, n + 1 のどちらか一つは 9 の倍数、どちらか一つは 11 の倍数 出なければいけない。（どちらか一つが 99 の倍数である場合も含む） 　以上の条件を満たす n-1, n+1, x, y を探すと以下の通りになる。 n-1, n+1 x y 88, 90 20 25, -64 108, 110 30 25, -84 196, 198 98 1, -196 y は 0 以上でなければいけないため、問題の条件を満たす (x, y) は (x, y) = (20, 25), (30, 25), (98, 1) の３組である。以上から４桁の整数は 2025, 3025, 9801 の３個である。

　試験会場は至って普通のカフェ。しかし試験問題は２０分で４５問というハードな内容。木村さんは無事試験に合格できたのか？ちなみに芸能界でメンサに入っているのはロザン宇治原のみ（あの人何やってんだ…）

　今回は入会テストの模試形式でメンバーは問題に挑む。問題は５問、時間は１０分間、どの問題から解き始めても良い。はたして何問解くことができるのか？

第１問：５組の家族が図のような距離で離れて暮らしています（黒字は２点間の距離、青字の数は家族の人数） 　５組の家族が一か所に集まるとき、移動距離の合計が最も短くなるのはどこの場所に集まるときでしょう？

第２問：トランプ５２枚をランダムに並べて ダイヤのＡ〜Ｋ，クラブのＡ〜Ｋ，ハートのＡ〜Ｋ，スペードのＡ〜Ｋ， の順番に並ぶ確率は何回に１回でしょう。この回数より多いものを以下のア〜カの中から選びなさい。 ア．紀元前5万年以降の人類 (約1000億人) が全て100歳まで生きたとして、 　　生涯に持った細胞ののべ個数 イ．全世界の金を集めて、ラスベガスのスロットマシン (1回 25セント) を 　　トライ出来る回数 ウ．宇宙にある全原子の総数 エ．全世界60億人の人間が、宇宙のはじめから現在まで1秒に1回ずつ 　　トランプを並べ続けたとしたときの総回数 オ．オセロゲームの考えられる差し手の総数 カ．64枚からなるハノイの塔の最小移動手数

第３問： 　Ａさんの家の北３ｋｍのところにＢさんの家があります。 　Ｃさんの家はＤさんの家の西に５ｋｍのところにあります。 　Ｅさんの家の南東方向にＡさんの家が見えます。 　Ｄさんに家の窓からＣさんの家の向こうにＥさんの家があります。 　Ａさんの家とＤさんの家の間には山があり見えません。 　Ｂさんの家から北西方向にＣさんの家が見えます。 　このとき、Ｃさんの家はＥさんの家のどの方角に何ｋｍのところにあるでしょう？

第４問：次の計算式の暗号を解き、できる２文字の漢字を下の５つの中から選びなさい。 3.5 ＋ 17.3 ＋ 3.7 ＋ 11.3 ＋ 2.6 ＋ 41.1 ＝ １．天才　２．天気　３．青空　４．空腹　５．東大

第５問：下の５枚のカードと＋、−、×、÷ の４つの記号を１回ずつ使い、答えが２１となる計算式を使いなさい。 　ただし、カッコは使えません。またＡ＝１，Ｑ＝１２とする。

　正解の前に各組の正解数を発表。

コマ大チーム	２問正解	第１，４問を正解
マス北野	１問正解	第５問を正解
木村・山田ペア	４問正解	第１，３，４，５問を正解

第１問：アが正解。単純に総移動距離を計算すればよい。 アに集まる：1×1 + 2×2 + 2×4 + 1×14 = 27 イに集まる：7×1 + 2×1 + 2×3 + 1×13 = 28 ウに集まる：7×2 + 1×1 + 2×2 + 1×12 = 31 エに集まる：7×4 + 1×3 + 2×2 + 1×10 = 45 オに集まる：7×14 + 1×13 + 2×12 + 2×10 = 155 実は、コマ大でこれと似た問題が出されたことがあります。詳しくは…ご自身でお調べください。私はそれを覚えていたのですぐ分かりました。

第２問：ウが正解。トランプの並びの確率は 1 / 52! ≒ 1 / 10^68 ア〜カの数をフェルミ推定で求めてみると ア：全人類の細胞の数 4 × 10^27 イ：スロットマシンをする回数 4 × 10^19 ウ：宇宙の原子の数 1 × 10^80 エ：人類がトランプを並べる回数 3 × 10^27 オ：オセロの指し手 1 × 10^60 カ：ハノイの塔の手数 2 × 10^29 この中で 10^68 より大きい値はウのみ。私は勘で当てました

第３問：Ｃの家はＥの家の東に３ｋｍのところにある。 　条件を満たすＡ〜Ｅの家の位置関係を図にすると以下の通りになる。 この図からＣの家はＥの家の東側にあり、２つの家の距離はＡとＢの間の 距離と同じく３ｋｍである。 （Ｄの家の位置は異なる場合もあるが解答には影響はない）

第４問：４が正解。計算式の各小数を点の両端で掛け算をすると ３×５ １７×３ ３×７ １１×３ ２×６ ４１×１ １５ ５１ ２１ ３３ １２ ４１ さらに各値の１０の位を五十音の「あ、か、さ…」、１の位を「あ、い、う…」に充てると １５ ５１ ２１ ３３ １２ ４１ お な か す い た 「おなか すいた」ということで４．空腹が当てはまる。これも竹内先生からのヒントでわかりました。

第５問：以下の計算式が正解。＋、−の順序が異なるものもあるが、×、÷は以下の方法しかない。 分からなかった。ん〜〜もう少し時間があれば解けたかも…