紹介された本は以下の通り。

木村美紀さん：グレゴリー・Ｊ・チャイティンの「セクシーな数学−ゲーデルから芸術・科学まで」

「数学はセクシーである」という考えのもとに数学の内容を紹介している。 「情報理論がもっともセクシーだとリオのカーニバルを見てひらめいた」 「数学の証明は抱く感覚に似ている」 など独特の表現を用いている。

〆サバアタル：ポール・ホフマンの「放浪の天才数学者エルデシュ」

「３歳で３桁同士の掛け算を計算できた」という伝説を持つ数学者ポール・エルデシュについて書かれた本。 　数学に関しては天才であったが、家や財産もなく放浪生活を続けるなど変人ぶりもまた有名であった。

中村亨先生：Oliver Byrne の「ユークリッド原論」

紀元前３世紀に書かれたユークリッドの「原論」。 　ハードカバーの装丁や色を使った解説図などが使われている。

菊川怜さん：手塚治虫の「ブラックジャック」

難しい外科手術に挑む医師ブラックジャックを描いた漫画。 　手塚さんは医学部出身ということで、その知識を生かした作品になっている。

菊川怜さん：菊川怜の「菊川怜の数学生活のススメ」

数学が生活の中で役に立っていることについて述べた本。 　相手の携帯電話の番号を探り当てる方法なんかも書かれている。

　一通り本の話が出たところで 「コマ大数学科公認副読本　THE PARADOX　 ザ・パラドックス」 のご紹介。マス北野・竹内薫・中村亨の３氏の鼎談の内容に加え、論理問題を掲載。今回は問題の中からいくつかご紹介。

問題１： 　ガダルカナル・タカさんは２つの封筒Ａ，Ｂを持っています。２つの封筒にはお金が入っており、一方の封筒のお金はもう一方の封筒のお金の２倍の金額が入っています（どちらが２倍かは不明） 　いまタカさんがＡの封筒を開けたところ１万円が入っていました。ということは封筒Ｂには「５千円」か「２万円」のいずれかが入っています。 　タカさんはＡ，Ｂどちらか一つだけ貰うことができます。一度決めたら変更はできません。また、 封筒Ｂの金額は手に持っただけでは分からないようになっています。 　タカさんはこのままＡのお金を貰ったほうが良いのでしょうか？それともＢに変更したほうが良いのでしょうか？

問題２： 　タカさんと無法松がトランプでゲームをしました。 ４枚のエースを使い、よくシャッフルし４枚を裏返します。無法松が４枚のうち２枚を選び、 　２枚が同じ色のカードならばタカさんの勝ち。 　２枚が違う色のカードならば無法松の勝ち。 とします。無法松はこのゲームに参加したほうが良いのでしょうか？

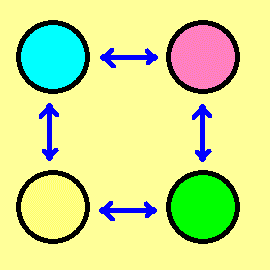
問題３： 　コマ大の出演者・スタッフ２３人全員がスタジオに閉じ込められました。 以下の事柄をしなければスタジオを出ることができません。 全員は一人ずつ楽屋に入り、お互いの連絡ができない。 一人がスタジオに入り、上の４つのランプの装置のボタンを押し、ランプを移動させる。 そして再び楽屋に戻る。 （ランプは矢印の間のみ移動できる。「青から緑」という対角線の移動はできない） この操作を繰り返すが、誰がスタジオに呼ばれるかはランダムに決まる。同じ人が繰り返し呼ばれることもありうるが、必ず全員一回は呼ばれる。 ある人がメインスイッチをオフにしたとき、一回でもランプを移動させた人のみがスタジオから脱出できる。 　楽屋に別れる前に、一度だけ話し合うことができる。全員が脱出できるためにはどのような方法をとればよいのでしょうか。ただし、最初に４つのランプのうちどこが付いているかは全員分かりません。 （呼ばれた回数とランプの状態から全員がランプを移動させたことが分かればＯＫ、ということみたい。呼ばれた回数ぐらいは教えてもらえると思う。）

問題１： 　Ｂの封筒の中身が「５千円」「２万円」である確率はそれぞれ１／２。このことから期待値を求めると 5000 × 1/2 + 20000 × 1/2 = 2500 + 10000 = 12500 となり、Ａの封筒よりも高くなる。よってＢの封筒に替えたほうが良い。

問題２： 　エース４枚から２枚を選ぶ方法は６通り。このうち２枚が同じ色となる組合せは「ハート、ダイヤ」「スペード、クラブ」の２通り。２枚が違う色となる組み合わせは４通り。 　よって、無法松が勝つ確率が高くなるため、参加したほうがよい。

問題３： 　……皆さんで正解をお考えください。どうしても知りたい方は「ザ・パラドックス」をお買い求めください（私も正解が分からない…）

問題： 　分を表す長針と時間を表す短針が同じ長さの時計があります。ある時刻でこの２本の針の位置から時刻を特定するとき、特定できない時刻があります。 その時刻は正午から１２時間の間に何回あるでしょう。 　（２本の針の長針・短針のとり方で２通りありますが、２通りともある時刻を表す場合がいくつあるかということ）

　マスも東大生チームも黙々と計算を続けた。しかし、２組の結果は大きく分かれた模様。

コマ大チーム	１３２回	時計を動かして検証
東大生チーム	１２１回	針の角度を使って計算？
マス北野	２回	正午と１２時の２通りしかない。

正解…１３２回　コマ大チーム正解！

長針（分針）は１時間に３６０°進み、短針（時針）は１時間に３０°進む。つまり長針は短針の１２倍の速さで進む。 　ある時刻の２本の針の位置で２通りの時刻のとり方があるとき、その２つの時刻の正午から進んだ短針の角度をそれぞれ θ、φ とすると θ≡12φ、φ≡12θ　(mod 2π) この２式から、 θ≡12 × 12θ = 144θ　(mod 2π) ⇒ 143θ≡ 0　(mod 2π) 0 ≦θ≦ 2πであるため、θ = (n/143)×2π と表すことができる。ここで n は整数で 1 ≦ n ≦ 143）を満たす。 2π が 360°つまり短針で12時間に対応するため、時間としては12時間の 1/143、およそ５分２秒ごとに 問題の条件を満たす時刻になる。もう一つ読み取れる時刻は正午からの時間の１２倍になる。

例えば 「０時　５分　２秒」は「１時　０分２５秒」とも読み取れる。 「０時１０分　４秒」は「１時１０分２９秒」とも読み取れる。 　　　　　　　　………………………… 「０時４５分１９秒」は「９時　３分４７秒」とも読み取れる。 　　　　　　　　………………………… 　しかし n = 13 のとき「１時５分２７秒」となり、これは２本の針が重なるため時刻の読み取り方は１通りしかない。このような場合は n が 13 の倍数のときに起こるため、全部で１１回起こる。この時刻は条件から外されるため、２通りに読み取れる時刻は 143 - 11 = 132 通りとなる。 　（例で挙げた時刻は「およそ」の時間です。実際は 「143 分の何」秒という値になります。）

問題： 　あなたは大学からの奨学金を受け取ることができる候補者の一人に選ばれました。 選考は以下の要領で行われます。 候補者全員の額に「緑」か「赤」の印を付ける。 額の印は自分の印は見えないが、ほかの候補者の印は見える。 自分以外の候補者の印を見て「緑の印が２個以上」見えたときのみ手を挙げる ようにする。 この後、自分の額の色が分かったら「わかりました」と試験官に答えを述べる。 　候補者はあなたを含めて４人います。あなた以外の３人全員の額には「緑」の印が付けられていました。 　あなたは手を挙げますが、ほかの３人も手を挙げました。しかし、しばらくは誰も「わかりました」といいませんでした。 　以上から、あなたの額の印の色とその推理の理由を述べなさい。

　マス、東大生チームは早々と解答が終了。前回に続き太神グヒオの新しい名前を考えることに、新しい名前は次回。解答は以下の通り、

コマ大チーム	緑	「２人以上」という言葉にちょっと考えるから？
東大生チーム	緑	背理法を２回使って考える。
マス北野	緑	自分が赤だとすぐにわかる人がいるから

正解…緑、全員正解！

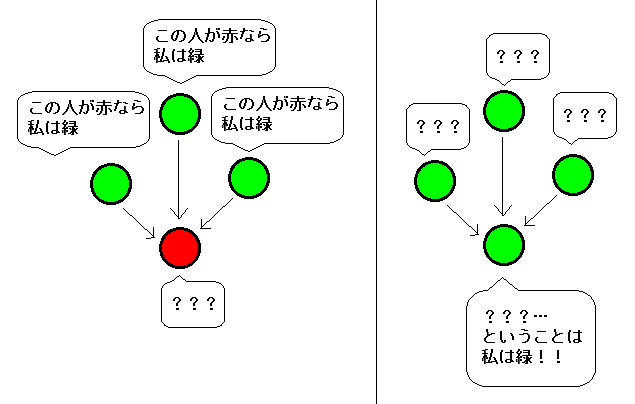
私の額の印が「赤」であるとき、全員が手を挙げる場合は「私以外の３人が緑の印」であるときのみ。 このため他の３人は私の額の「赤」の印を見て、すぐに各々の額に「緑」の印があることが分かるはず。 　しかし「しばらく誰も『わかりました』といいませんでした」ということは、上の考え方以外の場合であることを意味する。つまり「４人全員が緑の印」であること。よって私の額の印は「緑」

Question: Glue together 3 cubes, whose edges are 3, 6 and 9 centimeters long, at their faces. Find the minimum surface area.

問題： 　一辺の長さが３，６，９ｃｍの３個の立方体を面で張り合わせた立体を考えます。 　このような立体で表面積が最も小さくなる時の値を求めなさい。

コマ大チーム	６４８平方ｃｍ	実際に立方体を張り合わせて求めた。
東大生チーム	６４８平方ｃｍ	３個がそれぞれ隣り合う立体を考えた。
マス北野	６４８平方ｃｍ	３個がそれぞれ隣り合う立体を考えた。

正解…６４８平方ｃｍ、全員正解！

一辺が３ｃｍの立方体（赤）６ｃｍの立方体（青）９ｃｍの立方体（緑）を上の図のように それぞれを面で張り合わせたような立体が最小の表面積を持つ。 　この立体の正面方向の面積は３個の立方体の面の面積の合計である。 　この立体の右方向の面積は緑と青の立方体の面の面積の合計と等しい。 　この立体の上方向の面積は緑の立方体の面の面積と等しい。 それぞれ反対方向の面積も等しくなるため、この立体の表面積は上の３方向の面積の合計の２倍になる。 この値を計算すると 2×(3^2 + 6^2 + 9^2) + 2×(6^2 + 9^2) + 2×9^2 = 648 cm^2