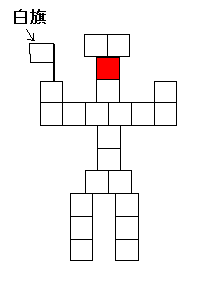
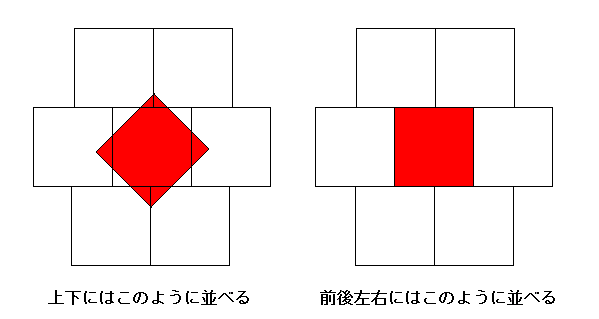
前後左右には右の図のように6個並べられるため合計20個。
「コマ大数学科」に挑む・11年12月
最終更新日2012年2月2日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| ホームズの謎(12/7) | |||||
| 視聴者からの挑戦状 (12/14) | |||||
| ルーレット(12/21) | |||||
| 250回記念(12/28) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
問題: 赤いサイコロが1個と同じ大きさの白いサイコロが多数あります。以下の条件で白いサイコロを並べたとき最大何個の白いサイコロを並べることができるでしょう。
|
|
コマ大チームチームの解答:
|
マス・ポヌペア、東大生チームの解答:
前後左右には右の図のように6個並べられるため合計20個。 |
正解…24個 全員不正解!
いわくつきの24個。どのように立方体が接しているのでしょう?
|
前後の面には真ん中の図のように7個接するように並べることができる。 最後に、左の面には6個接するように並べる。
以上から立方体の個数は4+7+7+6=24個となる |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年12月
「視聴者からの挑戦状 (12/14)」
|
問題: 1 〜 10 の整数を以下の条件を満たすように並べるとき、何通りの並べ方があるでしょうか: 並べたものを最初から2個ずつの数を「組」と呼ぶことにする。
|
| コマ大チーム | 84通り | 検証の結果 |
| 東大生チーム | 42通り | 奇数と偶数の組を探した。 |
| マス・ポヌペア | ??通り | すみません。解答を取り忘れました。 |
正解…84通り、コマ大チーム正解!
見事コマ大チームが正解を出した。解説は以下の通り。
|
10個の数字の組み分け、各組の順番を決めると問題の条件を満たす10個の数字の並びは3番目以降が決まる。 たとえば (1,2) (3,4) (5,6) (7,8) (9,10) と組み分けし、この順で順番を決めると各組とも偶数が大きいため、 「1, 2, 4, 3, 6, 5, 8, 7, 10, 9」,「2, 1, 4, 3, 6, 5, 8, 7, 10, 9」 という並べ方に決まる。同様に、(1,10) (7,8) (5,6) (2,3) (4,9) という組と順番を決めると「1, 10, 8, 7, 6, 5, 2, 3, 9, 4」,「10, 1, 8, 7, 6, 5, 2, 3, 9, 4」 という並べ方に決まる。 |
|
問題では最初の数字は順に 1, 6 としているため、残り8個の数字の組み分けと順番が何通りあるかを求めればよい。 さらに最後(10番目)の数字が 8 であるため9番目の数字は奇数。問題の条件からひとつ前の組(7,8番目)の大きい数は奇数であることが分かる。この条件を満たす組は 1, 6, 8 は使うことができないため、 (2,3), (2,5), (2,7), (2,9), (4,5), (4,7), (4,9) の7通りしかない。各組を決めるごとに
2,4,5番目の組の奇数の決め方に6通り。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年12月
「ルーレット (12/21)」
|
問題: A〜Fの6人が丸いテーブルの周りに図のように座っている。テーブルの中央にはルーレットがあり、ルーレットを回転して自分の前に来た数字を得点として加えていくゲームを行う。
|
| コマ大チーム | Aから順に 15, 14, 13, 10, 11, 12 | 検証の結果 |
| 東大生チーム | Aから順に 15, 11, 14, 10, 14, 11 | Aが逆転する得点を考えた |
| マス・ポヌペア | Aから順に 15, 14, 13, 10, 11, 12 | Aが 5,5,5 点を取ると 逆転できないことから |
正解…Aから順に 15, 14, 13, 10, 11, 12、コマ大チーム、マスペア正解!
各組とも、2回目の時点でAが最下位であることは分かっていた。そこからどう逆転するかはルーレットの数字の並びから考えることがポイント。
|
1回目の最高得点をとった人はCであるため6人の得点は
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ルーレットのむかい合う2つの点数の合計はいずれも5点。よってむかい合うAとDの5回目が終わった時の得点の合計は5×5=25点。Dはすでに9点を取っている。この状態でAが5回目に最高得点を取るためには以下の場合がある。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年12月
「250回記念 (12/28)」
|
問題: 半径1の円に内接する正6角形の頂点を時計回りにA1,A2…,A6と付ける。任意の3点を選んで三角形を作るとき、三角形の面積の期待値を求めなさい。 ただし、同じ点を2回以上選ぶときも含め、その時は面積は0とする。
|
250回を迎えても衰え知らずのマス北野、そして容赦しない東大生・秒殺シスターズ。着々と答えを導いていく。一方秘策を受けたコマ大チームは鉛筆をコロコロ転がしていた。鉛筆で3個の頂点を決めて、面積の期待値を地道に求める作戦に出た。時間内にどこまで正解に近づけるか?
| コマ大チーム | 0.36808 | 鉛筆を転がした結果 |
| 東大生チーム | √3/4 | 作られる三角形の面積を 元に計算。 |
| マス・ポヌペア | 4√3/7 | 作られる三角形の面積を 元に計算。 |
正解… √3/4 東大生チーム 見事正解!
東大生チーム文句なしのコマ大フィールズ賞であった。解説は以下の通り。
|
6点から任意の3点を選ぶ方法は同じ点を複数回選ぶ場合も含めて 6×6×6 = 216 通りある。このうち三角形を形成する選び方、そして三角形の面積は以下のとおりである。
36 × √3/4 + 72 × √3/2 + 12 × 3√3/4 = 9√3 + 36√3 + 9√3 = 54√3 上の合計の値を 216 で割ると期待値が求まる。54√3 / 216 = √3/4 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年12月