六角形の形をした紙を図のようにハサミで切り 並べ替えて正方形にした(ハサミを入れたギザギザの 数は6個です)
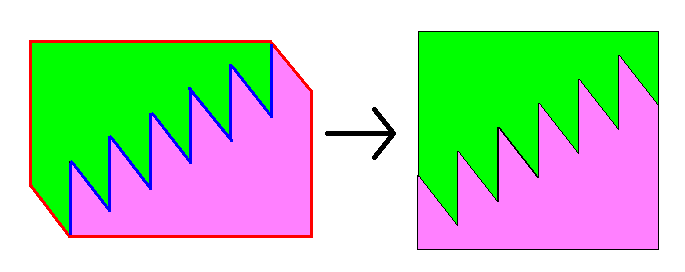 六角形の周囲が70cm(赤線の部分)ハサミの切り口の長さが61cm(青線の部分)
であるとき、正方形の一辺の長さを求めなさい。
六角形の周囲が70cm(赤線の部分)ハサミの切り口の長さが61cm(青線の部分)
であるとき、正方形の一辺の長さを求めなさい。
「コマ大数学科」に挑む・12年2月
最終更新日2012年3月31日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 英語で数学 Part 6 (2/1) |
| 裁ち合わせ (2/8) |
| 必勝法 Part 7 (2/15) |
| 作図問題 (2/22) |
| 平均値の定理 (2/29) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
Question: Six mattresses are stucked in a warehouse. Each mattress was originally 12 cm thick but thickness is reduced by one third each time an additional mattress is piled on top. What is the height of the stack? |
|
問題: 倉庫にマットレスが6枚重なっています。 マットレス1枚の厚さは12cm。しかし、 上に1枚マットレスが載ると、厚さは1/3に縮まる。 このとき、6枚のマットレスの高さはいくつになるでしょう? |
今回の東大生チームは前回英語が今一つであることが判明した杉山・瀬戸山ペア。しかし、いざ問題となると一変。着実に問題を把握し、答えを導いていく…と思ったが?
| コマ大チーム | 17.9 cm | 検証の結果 |
| 東大生チーム | 2660/81 cm | マットレスは「1/3分縮まる」 と考え計算。 |
| マス・ポヌペア | 32.8 cm | マットレスは「1/3分縮まる」 と考え計算。 |
正解…2660/81 (およそ 32.83) cm 東大生チーム、マス・ポヌペア正解!
コマ大チーム、努力もむなしく不正解。改めて正しい問題文と解説です。
|
問題: 倉庫にマットレスが6枚重なっています。 マットレス1枚の厚さは12cm。しかし、 上に1枚マットレスが載ると、厚さは1/3だけ縮まる。 (つまり厚さは2/3になる) このとき、6枚のマットレスの高さはいくつになるでしょう? |
|
マットレス1枚の厚さは 12 cm。この上にマットレスを1枚載せると
下のマットレスは 12 cm の 2/3、つまり 8 cm となる。上のマットレスは 12 cm のまま。
この2枚の上にさらにマットレスを1枚載せると、 マットレスは一番上は 12 cm で、下は一つ上のマットレスの厚さの 2/3 になる。以上から 6枚重なっているときの厚さの合計は 12 + 8 + 16/3 + 32/9 + 64/27 + 128/81 = 2660/81cm |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年2月
「裁ち合わせ (2/8)」
|
問題: 六角形の形をした紙を図のようにハサミで切り 並べ替えて正方形にした(ハサミを入れたギザギザの 数は6個です)
|
ひらめきで勝負のマス北野。一方東大生チームは秒殺シスターズ。計算で答えを求めようとするが 何やら長い計算式が現れた。正解にたどり着けたのか?
| コマ大チーム | 18cm | 検証の結果 |
| 東大生チーム | 18cm | 方程式を作って解いた。 |
| マス・ポヌペア | 17cm | 90の半分45の約数 から考えた。 |
正解…18cm コマ大チーム、東大生チーム正解!
私のことは放っておいて解説です。
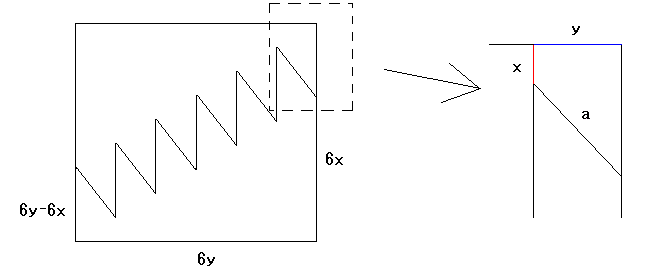 上の図のように切り取り線の縦の線から周囲の辺へまっすぐ線を引き、辺までの距離を x, 辺の交点から正方形の頂点までの長さを y, 切り取り線の斜め線の長さを a とする。
上の図のように切り取り線の縦の線から周囲の辺へまっすぐ線を引き、辺までの距離を x, 辺の交点から正方形の頂点までの長さを y, 切り取り線の斜め線の長さを a とする。このとき正方形の一辺の長さは 6y, 頂点から切り取り線の交点までの長いほうの距離は 6x, 短いほうの距離は 6y-6x となる。この短いほうの距離は切り取り線の縦方向の長さと同じである。
問題の図から、六角形の周囲の長さは 2*(6x+6y+a), 切り取り線の長さは 6(6y-6x)+5a となる。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年2月
「必勝法 Part 7 (2/15)」
|
問題 以下のルールに従ってゲームを行います。このゲームの必勝法を見つけなさい。
|
必勝法を見出すためにマスが取った行動は消しゴムを先手・後手の位置に置き実際に動かしていった。東大生チームは消しゴムではなく鉛筆で位置を指しながら思案する。各組の解答は以下の通り
| コマ大チーム | 後手が常に端にいるようにする と勝てる |
| 東大生チーム | 両者が3×3の対角線の位置に 入るようにする。 |
| マス・ポヌペア | 後手が相手と奇数だけ差をとる ようにする |
正解は…3組とも不正解。が…
マスが一言「3の倍数だけ離れれば勝てる」と話していた。この考え方から必勝法が見つけることができる。
|
どちらかが負けになるときは、両者が隣り合う(差が1である)2つの数字にいるときである。この時、両者の移動したマス目を数えると合計がちょうど98になる。つまり、先に移動したマス目の合計を98にすれば勝ちになる。 たとえば、下の図のように先手が「53」後手が「54」に入った状態で勝負が決まった時、先手は 52 マス、後手は 46 マス移動しているため、合わせて 52+46 = 98 マス移動したことになる。
後手が1マス、または10マス移動したとき、先手は2マス、または20マス移動する。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年2月
「作図問題 (2/22)」
|
問題: 図のような四角形 ABCD と点 M がある。点 M を中心とする平行四辺形で4個の頂点が それぞれ AB, BC, CD, DA 上にある平行四辺形を作図しなさい。
|
万能の製図道具を手に解答に挑むコマ大チーム。しかし中村先生から「目盛を使わないように」という指摘から目盛を隠して平行四辺形を作る。マス・ポヌペアと東大生チームは正解の手掛かりとなる作図を始めた模様だが、マスはそれを消してしまった。はたして解答は
| コマ大チーム マス・ポヌペア | 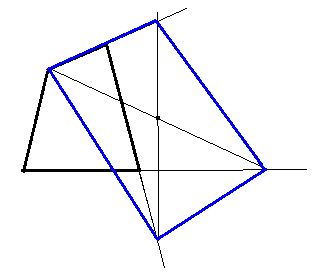
| 点Bを含む平行四辺形 を作った |
| 東大生チーム | 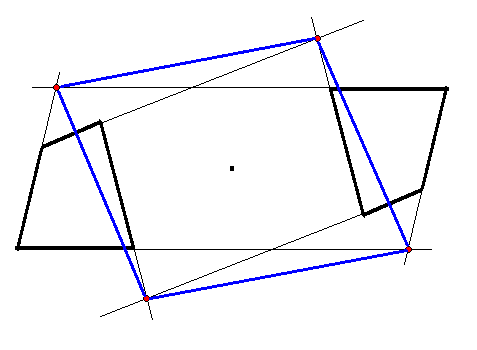 | 点Mで点対称な四角形を 描き作図した |
正解は…東大生の作図方法は正解です
コマ大チームやマスの作図の方法でも平行四辺形はできるが、一般の四角形に対してでは作図できない。東大生チームの作図の方法を詳しく説明。
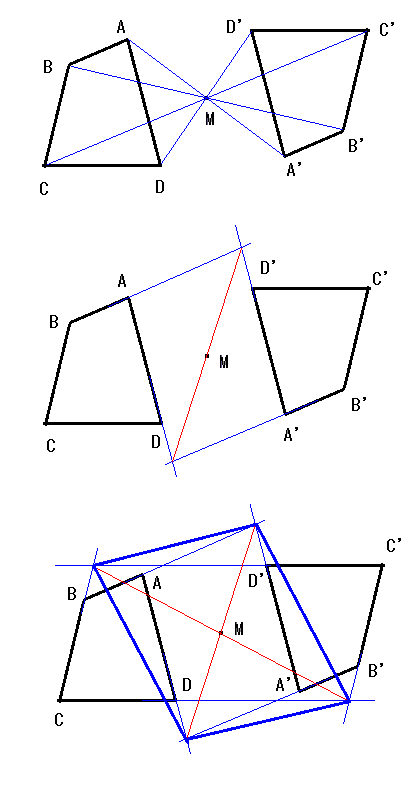 点 M に対して四角形 ABCD と対称な四角形 A'B'C'D' を描く。
点 M に対して四角形 ABCD と対称な四角形 A'B'C'D' を描く。
これら4個の交点からなる四角形は2本の対角線が中点 M で交わるため平行四辺形になる。 |
|
問題の四角形において、交わる2直線として BC と CD, AB と AD の2組に対して上と同じ作図をすると点 M を 中点とする2本の線分が求まり、2本の線分(図の赤い線)を対角線とする平行四辺形が問題の条件を満たすことが分かる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年2月
「平均値の定理 (2/29)」
|
問題: 自動車で北東の方角にあるゴールに向かいます。ゴールまでの到着の間、 自動車の鼻先が一度も北東を向くことなく進む場合のルートを作図しなさい。 (自動車はバックをしてはいけません)
|
今回の問題、即答したのは秒殺シスターズ。答えの図をさっと描いて、念のための確認作業。一方のマス北野は「平面上で答えを出すのか」と質問。おそらく地球をぐるっと回るルートを考えていたらしい。
|
こんなルートを考えていたのかも…
|
|
|
正解…3組とも正解!
さて「平均値の定理」はどこで出てくるのでしょう?
|
そこで左方向に転換すると、北東の方角を向くことなく車は北東より東に方向転換できる(右の図) 東大生チームやマス・ポヌペアは北東より東→北東より北という方向転換をしたルートを考えたが、この場合は方向転換に向きが逆になる。 |
|
「平均値の定理」とは問題の様にスタートからゴールまで移動するとき、必ず「スタートからゴール」
を結ぶ直線と平行な方向を向く、という定理。上の図では赤い矢印が平行な方向を向いているときである(本当はもっと解説が必要ですがこの位で勘弁) 今回の問題でもどのルートでも必ず「北東」に平行な方向を向くが、「北東」と反対方向の「南西」を向くこともある。これが答えの右の図のルートになる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年2月