問題： 　Ａ君とＢ君はそれぞれ２個ずつ正の整数を書きました。合計４つの整数は以下の条件が成り立ちます。 Ａ君の２つの整数の積はＢ君の２つの整数の和の２倍 Ｂ君の２つの整数の積はＡ君の２つの整数の和の２倍 Ａ君の２つの整数の和はＢ君の２つの整数の和以上である。 　このとき考えられる４つの整数の中でＢ君の２つの整数の和の最大値を求めなさい。

　東大生チームはすっかりベテランの木村さんが率先して計算を行う。何かをひらめいたのか一気に計算を進め「出た！出た！」と連呼した。マスはじっくり計算。

コマ大チーム	１３	Ｂ君は３と１０を選んだ。
マス・ポヌペア	１１	「３と６」という解答は見つけたが もう少し大きいのでは、と勘で解答
東大生チーム	９	Ｂ君は３と６を選んだ。

正解…２７　全員不正解！

Ａ君が書いた整数を a, b Ｂ君が書いた整数を c, d とする。問題の条件を式で表すと ab = 2(c + d),　　cd = 2(a + b),　　a + b ≧ c + d 　１番目の式と３番目の式から 　　　ab = 2(c + d) ≦ 2(a + b) 　⇒　ab - 2 a - 2 b ≦ 0 　⇒　ab - 2 a - 2 b + 4 ＝ (a - 2)(b - 2) ≦ 4 　a, b は正の整数であることから (a - 2)(b - 2) ≦ 4 を満たす a, b は以下の場合がある。

a = 1 であるとき、１番目の式と２番目の式から 　　　b = 2(c + d) = (cd - 2)/2 　⇒　cd - 4 c - 4 d ＝ 2 　⇒　(c - 4)(d - 4) ＝ 18 よって (c-4, d-4) = (1, 18), (2, 9), (3, 6) の３通り。それぞれの場合で b, c, d を求めると (a, b, c, d) = (1, 54, 5, 22), (1, 38, 6, 13), (1, 34, 7, 10) となる （c, d の値が逆の場合もあるが、問題では順序は考えなくてよい。b = 1 のときも c, d について同様の結果が得られる。）

a = 2 であるとき、１番目の式と２番目の式から 　　　b = c + d = (cd - 4)/2 　⇒　cd - 2 c - 2 d ＝ 4 　⇒　(c - 2)(d - 2) ＝ 8 よって (c-2, d-2) = (1, 8), (2, 4) の２通りがある。それぞれの場合で b, c, d を求めると (a, b, c, d) = (2, 13, 3, 10), (2, 10, 4, 6) （b = 2 のときも c, d について同様の結果が得られる。）

その他の a, b の場合のうち ab が偶数になるものは (a, b) = (3, 4), (4, 4), (3, 6) の３通り。 (a, b) = (3, 4) の場合は条件にあう c, d は見つからない。 (a, b) = (4, 4), (3, 6) の場合の条件にあう c, d はそれぞれ (c, d) = (4, 4), (3, 6) である。

以上の組み合わせのうち、c + d が最大になる組み合わせは (c, d) = (5, 22) のときで ２数の和は 27 になる。

問題： 　５×５の正方形が並んだ盤面に１０円玉３枚、１００円玉５枚を並べる。ただし 縦の列、横の列、斜め４５度の列に異なるコインが並ばないようにしなければいけない。 　このような並べ方を見つけなさい。 上の並べ方の場合、青の線上の縦と斜めの線に１０円と１００円が並んでいるため、条件に合わない。

　３チームとも試行錯誤しながら答えを導き出そうとしている。いち早く答えを出したのはマス・ポヌペア。自称「おっさん声」の瀬戸山さん率いる東大生チームも続けて解答。コマ大も時間ぎりぎりに答えを出した。

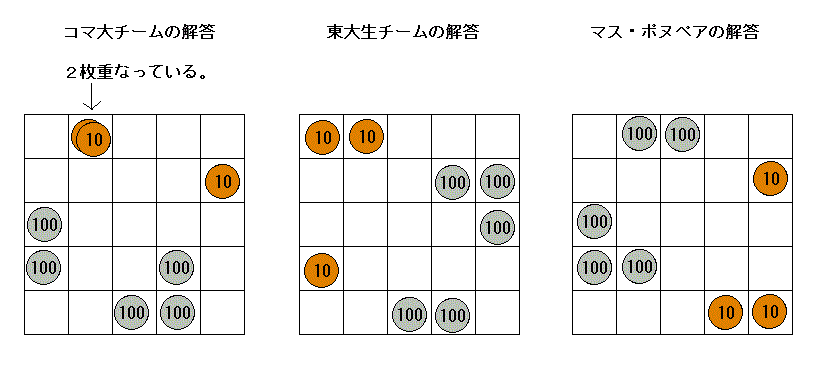
判定は…マス・ポヌペア、東大生チーム　正解！！

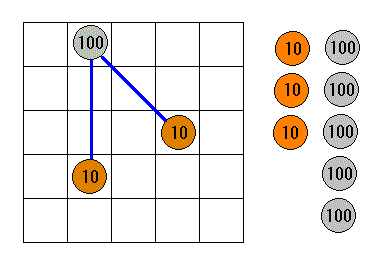
１０円玉を置いたとき、１００円玉が置けなくなるマス目の数を調べると下左の図の通りになる。 この数字が少ないところに１０円玉を置くとよい。（空欄のマス目は対称性から数が分かる） 　左上隅のマス目に１０円玉を置いた時を考える。２枚目の１０円玉は１枚目の１０円玉と同じ列に置くことがよいと見る。２枚目の１０円玉を置いたときに、さらに１００円玉が置けなくなるマス目の数を調べると下右の図の通りになる。

先ほどの図で「５」の描かれたマス目は２個ある。それぞれのマス目に１０円玉を置いたとき、３枚目の１０円玉を置いて１００円玉が置けるマス目の数を調べると以下の通りになる。 　どちらの場合でも１００円玉が５個置けることができないことが分かる。 　「５」の描かれたマス目として、１枚目の１０円玉と隣り合うように２枚目の１０円玉を置く。このとき３枚目の１０円玉を置いて１００円玉が置けるマス目の数を調べると以下の通りになる。「５」と書かれたマス目が１個だけある。ここに３枚目の１０円玉を置けば１００円玉を５枚置くことができる。 　他の場合についても調べても５枚の１００円玉を置く並べ方はできない…みたい。

問題： 　Ａ君とＢ君はあるゲームを行います。ゲームに勝つとそれぞれ相手からコインを１枚もらうことができます。どちらかがコインをすべて取るとゲームは終了です。 　現在コインをＡ君は６枚、Ｂ君は２枚持っています。ゲームに勝つ確率がＡ君が１／３、Ｂ君が２／３であるとき、Ａ君がＢ君のコインをすべて取る確率を求めなさい。

　コマ大と同様に苦戦している東大生チームとマス・ポヌペア。着実に計算をして確率を求めようとするが、すっきりとした値が出てこない。時間内に答えが出たのでしょうか？

コマ大チーム	１／４	８回行い２回Ａが勝った
マス・ポヌペア	１０％	ポヌさんがこつこつと計算したが、 最後は「何となく」
東大生チーム	数値は出ず	ボードには「a_{n+2}=3/5 + 2/5 a_n」 これを解けば求まるとのこと。

正解… 21/85 全員不正解！

Ａ君がコインを n 枚、Ｂ君がコインを 8-n 枚 持っているとき、Ａ君がＢ君のコインをすべてとる確率を P(n) と表す。 　n = 0 のときはＢ君の勝ちであるため、P(0) = 0 　n = 8 のときはＡ君の勝ちであるため、P(8) = 1. その他の場合、 　Ａ君が勝つとコインが１枚増えるためこのあとＡ君が勝つ確率は P(n+1) に変わる。 　Ｂ君が勝つとコインが１枚減るためこのあとＡ君が勝つ確率は P(n-1) に変わる。 ゲームに勝つ確率を考えると P(n) = 1/3 P(n+1) + 2/3 P(n-1) という式が成り立つ。

問題： 　四角形 ABCD について、図のように角度が定められたとき、 ∠ADB を求めなさい。

　東大生チームは研究生として今回は溝田さんが登場。山田さん以来の右利き、左利きペアで解答に挑む。マス・ポヌペアもあれやこれや線を引いて行って答えを導き出す。

コマ大チーム	１５度	図を描いて角度を測った。
マス・ポヌペア	１０度	あちらこちら線を引いて出てきた。
東大生チーム	３０度	逆さの正三角形を作って 考えた。

正解…１０度　マス・ポヌペア正解！

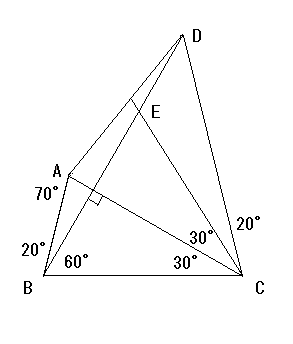∠ACB = 30°, ∠DBC = 60°より対角線 AC, BD は直交する。また ∠BAC = 180°- 30°- 20°- 60°= 70° となる。 さらに BD 上の点 E を ∠BAC = 30°となるように定めると 三角形 BCE は正三角形になる。さらに ∠BCA = ∠ECA, BC = EC, AC = AC であることから二つの三角形 BCA, ECA は合同である。

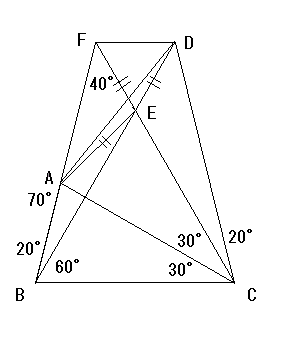AB と CE の交点を F とする。このとき ∠BCF = ∠CBD, ∠CBF = ∠BCD, BC = CB より二つの三角形 BCF, CBD は合同である。このことから F から BC への距離 = D から BC への距離 であることが分かるため、四角形 BCDF は FD // BC の等脚台形である。 　三角形 BCA, ECA は合同であることから ∠EAC = ∠BAC = 70° よって ∠FAE = 180°- ∠BAC - ∠EAC = 40°= ∠AFE つまり三角形 AEF は AE = FE の二等辺三角形である。また三角形 DEF について FD // BC であることなどから３つの角がすべて 60° であるため、正三角形である。このことから AE = FE = DF が成り立つため、三角形 ADE もまた二等辺三角形であり、∠EAD = ∠EDA が成り立つ。 　三角形 ABD の内角の和を求めると 　∠ABD + ∠BDA + ∠ADB = 20°+ ∠EDA + (70°+ 70°+ ∠EAD) = 160°+ 2∠EDA この値は 180°であるため、∠BDA = ∠EDA = 10°であることが分かる。

問題： 　階段を一歩で１段または２段上がっていきます。ただし、 連続して２段上がることはしません。 　この条件で１５段昇る方法は何通りあるでしょうか？

n 段ある階段を問題の条件を満たすように昇る方法が A_n 通りあるとする。 　ある昇り方で最後に１段昇るか２段昇るかで場合分けをする。 　最後に１段昇る昇り方は、それまでの n-1 段は条件を満たす昇り方で あるため、A_{n-1} 通りある。 　最後に２段昇る昇りとき、２回続けて２段ずつ昇ることはできないため、 最後から２番目は必ず１段昇る。 　つまり最後に２段昇る昇り方は、それまでの n-3 段は条件を満たす昇り方にして、 そのあと１段、２段という昇り方になるため、A_{n-3} 通りある。 　以上から A_n については A_n = A_{n-1}+A_{n-3} という関係式が成り立つ。 　A_1 = 1, A_2 = 2, A_3 = 3 より以降の計算を続けると A_4　= A_3　+ A_1　= 4 A_5　= A_4　+ A_2　= 6 A_6　= A_5　+ A_3　= 9 A_7　= A_6　+ A_4　= 13 A_8　= A_7　+ A_5　= 19 A_9　= A_8　+ A_6　= 28 A_10 = A_9　+ A_7　= 41 A_11 = A_10 + A_8　= 60 A_12 = A_11 + A_9　= 88 A_13 = A_12 + A_10 = 129 A_14 = A_13 + A_11 = 189 A_15 = A_14 + A_12 = 277 　以上から１５段昇る方法は 277 通りであることが分かる。