数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月
「コマ大数学科」に挑む・12年6月
最終更新日2012年7月18日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「コラッツの定理 (6/1)」
数学では解決されていない問題に懸賞金がかけられることがある。今回のテーマ「コラッツの定理」にも懸賞金が掛けられている。その額、何と!500ドル(日本円で約4万円)金額はともかく問題を解き後世に名を残してはいかがでしょうか?
問題:
1より大きい整数に対して以下の操作を行い、計算結果が1になるまで
繰り返します。
- 整数が偶数のとき、その数を2で割る。
- 整数が奇数のとき、その数に1を加える。
整数 n に対して、上の操作を行い1になるまでの操作の回数を f(n),
整数 N に対して、f(1) から f(N) の和を g(N) と表します。
このとき g(32) を求めなさい。
例えば、3 から始めたとき、
3 → 3+1 = 4 → 4/2 = 2 → 2/2 = 1
と3回の操作で1になるため f(3) = 3。ただし f(1) = 0 として考える。
|
労働者代表(?)のコマ大チーム。今回は日ごろの憂さを晴らすためにビールを飲みながら検証。
ビールをたくさんのコップに注ぎ、問題の通りにコップの個数を増減させながらコップ1杯になるまで回数をひたすら数える。もちろん「2で割る」ときコップのビールは飲み干す。始めはビールを飲みながら日ごろの愚痴を話していたが、次第に愚痴が激しくなるとともに飲み干すビールの量も増えていった。様々な意味で久しぶりの長丁場の検証となりました。
ビールがなくても問題は解ける…あたりまえだけど。計算用紙に数を書き並べていく両チーム。なにがしかの法則が見つかればよいが決め手がないまま時間が過ぎていった。
| コマ大チーム | 178 |
検証の結果。しかし酔っていたので
数え間違いがあるかも? |
| マス・ポヌペア | 175 | ポヌさんと分担してひたすら数えた。 |
| 東大生チーム | 178 | ひたすら計算した。
もう少しで漸化式ができそう… |
何か法則があるか探していたマス・ポヌペアと東大生チームだったが見つからず。結局は一つ一つ計算して合計を求めた。私もこつこつと計算をして「178」と出た。
正解…178 コマ大チーム、東大生チーム正解!!
東大生瀬戸山さんが漸化式を導き出そうとしたが、今一歩届かず。この問題、以下のような漸化式があります。
|
f(n) の値を並べると以下の結果となる。
g(N) には以下のような漸化式があります。
g(2N) = 2*g(N) + 3*N - 2
例えば上の表から g(3) = 4, g(6) = 15 となる。このとき
g(2*3) = 2*g(3) + 3*3 - 2
が成り立つことが分かる。この漸化式を使い 2 のべき乗の数の g(N) の値を求めていく。
g( 4) = 2*g( 2) + 3* 2 - 2 = 6
g( 8) = 2*g( 4) + 3* 4 - 2 = 22
g(16) = 2*g( 8) + 3* 8 - 2 = 66
g(32) = 2*g(16) + 3*16 - 2 = 178
これで g(32) = 178 という答えが出てくる。
|
上の漸化式の証明は帰納法を使います。
- N = 1 のとき上の表から g(2) = 2*g(1) + 3*1 - 2 であることが分かる。
- g(2N) = 2*g(N) + 3*N - 2 が成り立つときに、N を N+1 に替えても成り立つことを
証明する。f(2N+1) と f(2N+2) を考える。2N+1 から操作を始めると
2N+1 → (2N+1) + 1 = 2N+2 → (2N+2) / 2 = N+1
となり以降は N+1 から始める操作であるため、f(2N+1) = 2 + f(N+1) と表される。同様に
2N+2 → (2N+2) / 2 = N+1 より f(2N+2) = 1 + f(N+1)
となるため
g(2N+2) = g(2N) + f(2N+1) + f(2N+2)
= 2*g(N) + 3*N - 2 + [2 + f(N+1)] + [1 + f(N+1)]
= 2*g(N) + 3*N - 2 + 2*f(N+1) + 3
= 2*g(N+1) + 3*(N+1) - 2
つまり N を N+1 に替えても式は成り立つ
|
今回のコマ大フィールズ賞はコツコツと答えを出した東大生チーム。それにしてもコマ大チームはビールを何杯飲んだのだろうか?
今回のテーマ「コラッツの定理」とは以下のようなもの。
1より大きい整数に対して以下の操作を行う。
- 整数が偶数のとき、その数を2で割る。
- 整数が奇数のとき、その数を3倍して1を加える。
このとき、すべての整数が有限回の操作で1になる?
|
ちょっと計算していくと必ず最後に「1」になるのですが、この証明は分かっていません。皆さん証明考えてみますか?
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月
「シンメトリー (6/8)」
前回研究生として出演した東大生本杉さん。正解が出せなかったため、今回こそは、と再び登場。
問題:
3つの角が90°, 60°, 30°の直角三角形を2つの線対称の図形に分割する。たとえば
下の図のような分割の方法がある。これ以外の分割を見つけなさい(分割の線は
折れ線でも可)
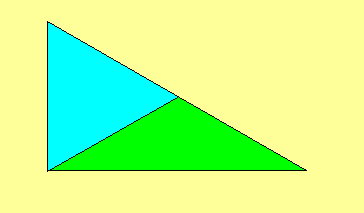
|
今回もコマ大チームはスタジオで答えを見つけることに。その前の練習(?)として現れたのは数学戦隊コマレンジャー。コマ大チーム扮するこの集団が様々な物を線対称の形にしていく。普段目にする看板の文字や建物、もちろん彼ら自身も線対称にする。ただ、練習になったかどうかはわからない。
一番手で答えを見つけたのはマス北野。竹内先生が「ひらめきの問題」と言っていただけに、さすがマスは早かった。その次にやっとで(?)見つけたのは木村さん。角度や長さを調べて線対称の分割を見つけた。さあ、本杉さんは見つけられたのか?

判定
マス・ポヌペア 正解!
東大生チーム 上の分割は正解!
東大生チームの下の解答は本杉さんの解答。今回も正解を出せず。まあ、私はまったく正解を出せませんでした。問題の例を含め3通りの分割が出ましたが、5通りの分割が分かっています。
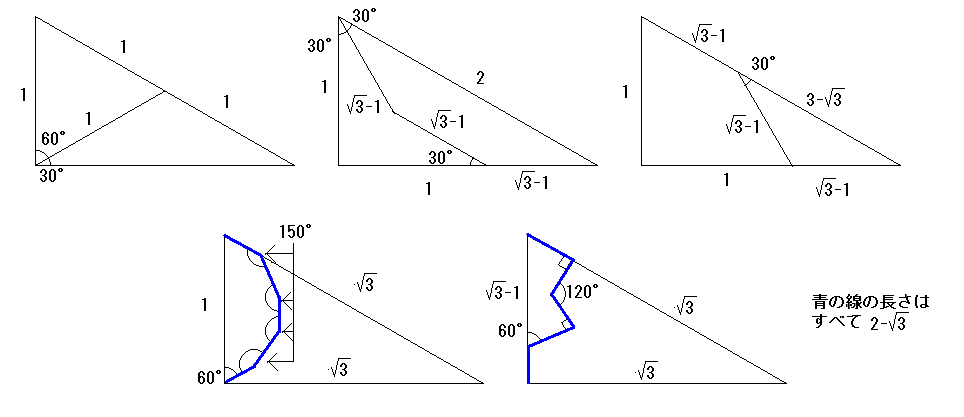
コマ大フィールズ賞は難易度の高い解答を出したマス・ポヌペア
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月
「マジックトリック (6/15)」
再び登場の研究生横内さんは実はラジオパーソナリティーも務めたこともあり、さらにアナウンサー志望。一応先輩の戸部アナウンサーの目の前で答えを出すことができるのか?
問題:
図の盤面から隠された一つの数字を当てることができる。その方法を考えなさい。

|
コマ大チームはトリックを見破るためマジシャンの元に超短期弟子入り。訪れたのはテレビで大人気のマジシャン「からくりど〜る」さん。いつもの「その通りです〜〜」という口調で淡々とマジックを披露。このあとマジックのタネを見破り、今回の問題への対策(?)とした。
前回に続き「ひらめき」が鍵となる問題。やはりマスは早くも答えを導いた。一方東大生も数字の並びの法則を見つけ大喜び。
解答の前に各組が実際に隠した数字を当てることとなった。3組とも当てたがコマ大チームは意気揚々と4か所の数字を当てることに挑んだが最後の一個で失敗。さてそのタネとは?
| コマ大チーム | 4人で手分けして数字の並びを暗記 |
| マス・ポヌペア | 2×2の並びがどの場所でも20になる |
| 東大生チーム | 数字が1マスおいて増えたり減ったりしている |
コマ大チームの方法もできないことはないんですが……1人でやると覚えられないでしょう。
正解…マス・ポヌペアは正解!東大生チームも一応正解
問題の図の通り、2×2の数字の並びを見るとすべて4つの数字の和が20になる。このことから1つ隠された数字の周囲の3つの数字の合計を20から引けば隠された数字が分かる。
用意していた正解を出した、ということでコマ大フィールズ賞はマス・ポヌペアに渡った。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月
「じゃんけん (6/22)」
じゃんけんの掛け声は「じゃんけんポン」しかし新潟では「チエーロッエスッ」長崎では「ちょいちょいちょい」と地域によって掛け声が変わる。そんな豆知識と共に今回の問題。
問題:
A,B,Cの3人でじゃんけんを100回行った。99回目までの結果は以下の通り
あいこ…44回、1人勝ち…33回、2人勝ち…22回
100回行ったとき、3人が出した手を調べると、グー、チョキ、パーがそれぞれ100回ずつであった。
このとき100回目のじゃんけんの結果は何でしょう。
|
コマ大チームの検証は勿論じゃんけん。じゃんけん必勝法を伝授したコマ大チームが向かったのはAKB48の内田眞由美さん。AKBの選抜じゃんけん大会で優勝した内田さん、相手に不足なしとじゃんけん対決をしたが見事に全員負け。最後は内田さんも一緒にグー、チョキ、パーのカードを並べながら答えを見つけた……ん?何の検証だったんだ?
東大生チームは相手の傾向でじゃんけんの手を読む瀬戸山さんと、からっきし苦手な杉山さんペア。何やら長い方程式が出てきた。一方マスはじっと考え込む。
| コマ大チーム | 1人勝ち |
検証の結果。100回目は
パー、グー、グー |
| マス・ポヌペア | 1人勝ち | 「100」は3で割ると
1余るから? |
| 東大生チーム | 2人勝ち | 9回ごとに同じ結果が
出る、という推測から |
コマ大チームとマス・ポヌペアが同じ答え。しかしある程度検証した東大生チームも手抜かりはない様子。
正解…1人勝ち コマ大チーム、マス・ポヌペア正解!!
東大生チームが9回のじゃんけんの結果を調べていたが、落ち着いて調べるとこの方法でも解答が出てくる。一方方程式を使うと…
-
1人勝ちになる手は「グ、チ、チ」「チ、パ、パ」「パ、グ、グ」の3通り。
100回じゃんけんをした時のそれぞれの結果の出た回数を a, b, c とおく。
-
2人勝ちになる手は「グ、グ、チ」「チ、チ、パ」「パ、パ、グ」の3通り。
100回じゃんけんをした時のそれぞれの結果の出た回数を d, e, f とおく。
-
あいこになる手は「グ、グ、グ」「チ、チ、チ」「パ、パ、パ」「グ、チ、パ」の4通り。
100回じゃんけんをした時のそれぞれの結果の出た回数を g, h, i, j とおく。
このときグーの出た回数は a+2c+2d+f+3g+j となる。同様にチョキの出た回数を求めると 2a+b+d+2e+3h+j となる。ともに100回ずつで等しいため、
a+2c+2d+f+3g+j = 2a+b+d+2e+3h+j
⇒ a+b-2c-d+2e-f-3g+3h = 0
⇒ (a+b+c)-(d+e+f)= 3(c-e+g-h)
この式で a+b+c は1人勝ちの回数、d+e+f は2人勝ちの回数である。上の式から (a+b+c)-(d+e+f) は3の倍数でなければいけないが、99回目までの結果を見ると 33 - 22 = 11 。100回目にこの値が3の倍数になるためには、1人勝ちを一回増やして 34 - 22 = 12 としなければならない。
つまり100回目は1人勝ちになる。
|
では実際に100回のじゃんけんがどのように行えば条件を満たすことができるか。
-
あいこになる4通り「グ、グ、グ」「チ、チ、チ」「パ、パ、パ」「グ、チ、パ」
がそれぞれ11回ずつ出てくる。これであいこの結果は44回。
-
1人勝ちになる3通り「グ、チ、チ」「チ、パ、パ」「パ、グ、グ」
のうち「グ、チ、チ」が12回、残りの「チ、パ、パ」「パ、グ、グ」が11回ずつ出てくる。
これで1人勝ちの結果は12+11+11=34回。
100回目に1人勝ちのいずれかが出ると考えると、99回までに1人勝ちが33回でることになる。
-
2人勝ちになる3通り「グ、グ、チ」「チ、チ、パ」「パ、パ、グ」
のうち「グ、グ、チ」「チ、チ、パ」が7回ずつ。残りの「パ、パ、グ」が8回出てくる。
これで2人勝ちの結果は7+7+8=22回。
|
|
上の100回のじゃんけんの結果でグー、チョキ、パーが何回出てきたかを計算する。
あいこのときは3つとも44回ずつ出てくる。
1人勝ちのときはグー:12+22=34回。チョキ:24+11=35回。パー:33回である。
2人勝ちのときはグー:14+8=22回。チョキ:21回。パー:7+16=23回である。
以上からグー、チョキ、パーの出た回数の合計が100回ずつであることが分かる。
|
マスも正解を出したが、「曖昧な論」より証拠、ということでコマ大フィールズ賞はコマ大チーム。
蛇足ですが、私は2問続けて正解を出しました。蛇足ですが…
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月
「天秤 (6/29)」
今回の研究生は溝田さん。女子野球部所属ということで野球のジェスチャークイズで盛り上がったところで問題。
問題:
円盤の上に12枚の皿が等間隔に配置されています。同じ重さの重り5個を
皿の上の置き、傾かないようにするにはどのように置けばよいのでしょうか?
ただし、1枚の皿に2個以上の重りは置けません。

|
コマ大チームは大きな円盤を使って検証。まず円盤の下にコマ大チームの代表者が寝て、円盤の5枚のさらに同じ量の液体を入れる。見事釣り合えば正解だが、釣り合わない時は下の人に液体がかかってしまう。でもご安心?この液体は美肌効果がある物のため、かかった後はお肌つるつるである。何ともシンプルな検証だが、見事に釣り合う置き方を見つけた模様である。
即座にひらめいたのはマス北野。あっという間に答えを出した。苦戦する東大生をしり目に意気揚々のコマ大チームとマス・ポヌペア。しかし、問題がもう1問用意されていた。
問題(第2問):
円盤の上に12枚の皿が等間隔に配置されています。重さが10g、20g、30g、
40、50gの重り5個を
皿の上の置き、傾かないようにするにはどのように置けばよいのでしょうか?
ただし、1枚の皿に2個以上の重りは置けません。

|
次の問題は重りの重さがみな違う。再び計算を始めるマス北野。コマ大チームは紙の円盤に10円玉を置き、円盤の中心を鉛筆の上に乗せバランスを取ろうとする。東大生チームはいまだ1問目が終わらず。しかしあれやこれや当てずっぽで答えを出すうちに正解が出てきて即座に2問目。果たして決着は
まず第1問の解説と正解は以下の通り。
2個の重りはお互いに反対の皿に乗せると釣り合う。3個の重りは円周を3等分する位置の皿に乗せると釣り合う。
この2つの皿の位置を重ねると、5個の重りを乗せても釣り合う置き方が求まる。

|
全員が苦労して求めた答えは意外と簡単な考え方で求まるため、一同ビックリ。さて第2問の解答はどうなったか?
東大生チームも時間ぎりぎりで答えを出した。
正解…東大生チームの置き方が正解!!
見事な大逆転(?)当てずっぽで第1問を答えた東大生チームが第2問を正解!この問題も第1問の解説の方法を使うと答えを出すことができます。
|
「10gを2個」「20gを2個」「30gを3個」それぞれの場合の釣り合う置き方を考えて、それらを組み合わせると問題の重りの置き方ができる。

|
こちらもシンプルな解答のため、全員が唖然。ということでコマ大フィールズ賞は一応大逆転の東大生チーム。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年6月


