数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年7月
「コマ大数学科」に挑む・12年7月
最終更新日2012年8月23日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「折り紙 Part 3 (7/6)」
東大生チームの研究生は金子さん。コスプレをしてダンスをしている、ということでダンスを披露。負けじ?と登場したのはポヌさん。何はともあれ問題で対決をしてください。
問題:
長方形の紙を折って最大の面積を持つ正三角形を作りなさい。
|
先週同様シンプルな問題である。コマ大チームは問題に使う紙を作ることから始めた。以前文具にこだわってきたが今回は紙にこだわった。和紙に色つきの繊維を漉きこんで作る和紙を教えてもらいながら作っていった。4人が真剣に作った和紙で問題に挑む…?
コマ大チームは作った和紙で問題を解こうとしたが「もったいない」ということでコピーをとって、普通の紙で答えを出す…と思ったらいきなりコマ大チームがおまけ付きの正解を出した。続いてマスが正解。この2組に第2問が出題された。
問題(第2問):
長方形の紙から切り取ることができる最大の面積を持つ正方形の
半分の面積の正方形を作るには最低何回折ればよいか?
|
第2問が出される中、苦戦しているのは東大生チーム。第1問は解答はしたものの説明が不十分ということでやり直し。先週に続いて逆転はなるのか…って、こういう文章を書くときは大概逆転はならないんだよね。
まず1問目の解答は以下の通り
|
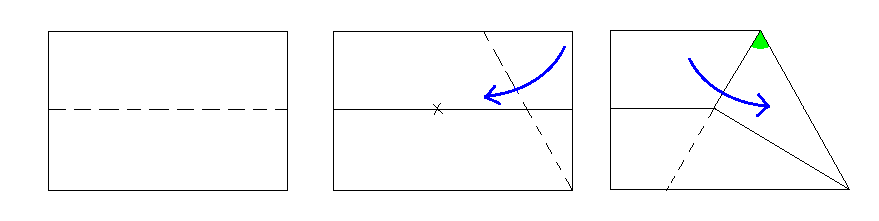
1.長方形の短い辺に対して半分に折る。
2.長方形の一つの辺を半分の折り目に合わせるように折る。
3.右の図の緑の部分が60°になるため、紙の端に合わせて折ると正三角形ができる。
|
|
2問目はコマ大チームとマス・ポヌペアが解答(図の数字は折る順番)
マスが始め「6回」と答えていたが、解説をしているうちに「4回だ」と解答を変更。
正解…3回 全員不正解
残念ながら全員不正解。どのように3回折って最大の正方形の半分の面積の正方形を作るのでしょうか?
|
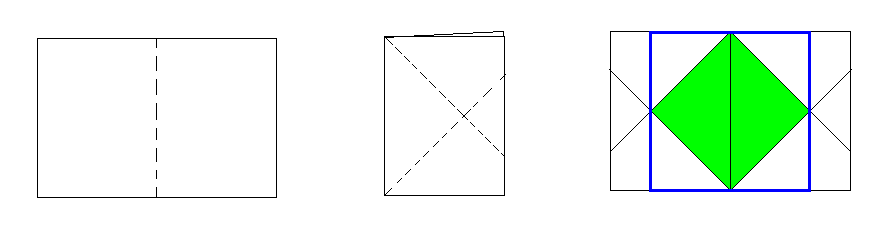
1.長方形の長い辺に対して半分に折る。
2.折り目の両端の角を半分に折る。
3.紙を広げると中央に半分の面積の正方形ができる(青の線は最大の正方形)
|
|
私も別の3回の折り方を考えていました。
|
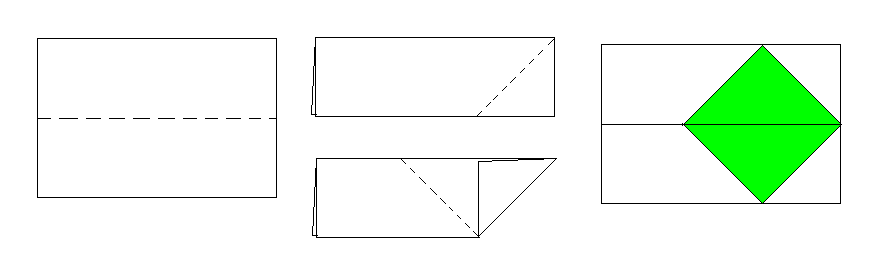
1.長方形の短い辺に対して半分に折る。
2.折り目の一方の角を半分に折る。
3.折った三角形に辺を合わせるように紙を折る。紙を広げると問題の正方形ができる。
|
|
こんなに意気揚々と書いていますが、1問目の作り方は分かりませんでした。実際に紙を折れば答えられたかもしれませんが… コマ大フィールズ賞は2問目で確実な正方形を作ったマス・ポヌペア。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年7月
「視聴者からの挑戦状 Part 3(7/13)」
東大生チームに新しい研究生、松本さんが登場。今回は視聴者からの出題。さて研究生の実力はいかに?
問題:
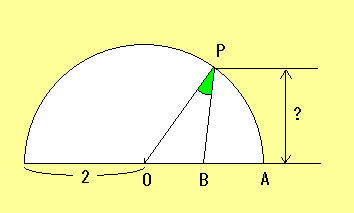
O を中心として OA = 2 を半径とする半円がある。B を OA の中点とし
半円の円周上に点 P をとる。∠ OPB が最大の値をとるときの点 P と OA
との距離を求めなさい。
|
コマ大では問題募集を始め、多くの事について視聴者からお便りをいただいてきた。そこで、問題の選定を兼ねてお便りを紹介した。進行はもちろんコマ大チーム+中村先生(選定係)東京名物大神本舗五百年のネタや東大生木村さんの恋人募集、以前出題した問題の別解についてもお便りが寄せられた。ここで中村先生が選んだ問題が上の問題である。今回はコマ大チームも一緒に問題に挑む。
半円にたくさんの線を引く3チーム。一気に答えを出したのはマス北野。ここしばらくのひらめきの速さには脱帽である。ある程度の目星をつけて計算式で答えを出すのは東大生チーム。手当たり次第角度を求めるのはコマ大チーム。三者三様の答えの出し方である。
| コマ大チーム | 1.72972927 | 点Pは点Bの真上にあると考えた。 |
| マス・ポヌペア | √3 | 点Pは点Bの真上にあると考えた。 |
| 東大生チーム | √3 | 点Pは点Bの真上にあると考えた。 |
3組とも点Pの位置は同じであるが、証明まで答えたのはマスのみ。
正解…√3 マス・ポヌペア、東大生チーム正解!
正解の証明のために、解説の中村先生が準備していたものは三角形の外接円を使った証明。一方マスは正三角形を使った証明を考えた。
|
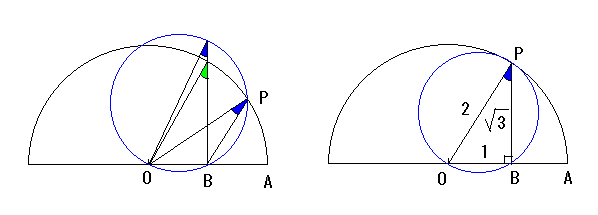
三角形 OPB の外接円を描いてみる。左の図のように外接円が半円と2点で交わるとき、外接円の内部に半円の円周が通っている。図の青で色づけされた2つの角度は等しく、また緑で色づけされた角度は青の角度よりも大きいことが分かる。
よって外接円が半円と2点で交わるとき、∠OPB より大きい角度を半円の円周上にとることができる。
このことから ∠OPB が最大の角度を持つときは外接円が半円と2点で交わらないとき、つまり外接円が半円と接するときになる。このとき三角形 OPB は ∠B が直角の直角三角形になる。
OP = 2, OB = 1 であることから、点 P の高さ(= BP)は √3 になる。
|
|
マスの解説は以下の通り
|
|
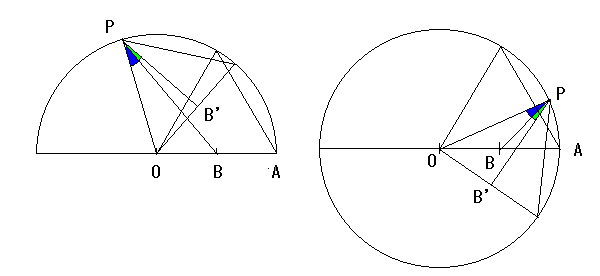
OP を一辺とする正三角形を描く。点 P から正三角形に垂線 PB' を下すと、∠ OPB' = 30°である。∠ OPB (図の青の部分) と ∠ OPB' の差を調べると、∠ OPB = ∠ OPB' - ∠ BPB' (図の緑の部分)
であることが分かる。
∠ BPB' が最も小さい値をとるときは ∠ BPB'= 0°のときであり、この時は三角形 OAP が正三角形になる。よって点 P の高さは√3 になる。
|
コマ大フィールズ賞は文句なしのマス・ポヌペア
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年7月
「必勝法 Part 8 (7/20)」
今回の東大生チームの研究生は大原さん。ミュージカルにも出演するという大原さん。舞台の上の度胸は発揮されるのか?
問題:
1から10の数字を使って二人でゲームをします。
二人は交互に一つずつ数字を書いていく。しかし、これまで書かれた
数字の約数は書くことができない。
最後に数字を書いた人が勝ちになるとき、このゲームの必勝法を考えなさい。
|
コマ大チームはとにかくゲームをして必勝法を探し出す。訪れたのはサブカルチャーの聖地?中野。この地域のお店の方にゲームに参加していただくことにした。ゲーム専門店やプロレスのマスクの専門店、メイドマッサージの店などの方にご協力いただき、ゲームを続ける。必勝法を見抜くことができたのか?
コマ大でこれまで出題されて「必勝法」の問題は7問。このうちマスは6問、コマ大チームは4問、東大生チームは1問正解している。今回もマスはひらめきで答えを出した。東大生チームも淡々と数字を書き並べていく。解答は以下の通り。
| コマ大チーム | 先手を選び複数個を選ぶ | 結果は敗北 |
| 東大生チーム | 後手を選ぶ | 結果は敗北 |
| マス・ポヌペア | 先手を選び「6」を選ぶ | 結果は勝利 |
ちなみに私は見当もつかず、勘で「先手が1をとる」と考えていた。私も東大生同様「必勝法」は苦手です(コマ大の検証で一度の複数個をとっていく理由を理解できませんでした)
正解…マス・ポヌペアの必勝法で正解!!
では詳細を…
|
先手が「6」を選んだあと残っている数字は
4,5,7,8,9,10
の6個。これらについて以下の方法で数字を選んでいく。
- 「4,5」のうち一方の数字を後手が選んだ時、もう一方を選ぶ。
- 「7,9」のうち一方の数字を後手が選んだ時、もう一方を選ぶ。
- 「8,10」のうち一方の数字を後手が選んだ時、もう一方を選ぶ。
後手からの数字の取り方の例として以下のようなものがある(カッコの中の数字は選べなくなる数字)
10(5)→ 8(4)→ 9 → 7
4 → 5 → 7 → 9 → 10 → 8
|
|
同様に、先手が「4」を選んでも先手の勝ちになる。このとき残っている数字は
3,5,6,7,8,9,10
の7個。これらについて以下の方法で数字を選んでいく。
- 「7、8」のうち一方の数字を選んだら、もう一方を選ぶ。
- 5を選んだら、6、9のうち一つを選ぶ。
- 6,9のうち一つを選んだら、5を選ぶ。
3、10については「6,9」のいずれかを選ぶ前か後かで選び方が変わる。
- 「6,9」のいずれかを選ぶ前であるとき、「3、10」のうち一方の数字を選んだら、もう一方を選ぶ。
- 「6,9」のいずれかを選んだ後であるとき(この時点で3は選べない)残っている数字と10のうち一方の数字を選んだら、もう一方を選ぶ。
後手からの数字の取り方の例として以下のようなものがある
7 → 8 → 3 → 10(5)→ 9 → 6
7 → 8 → 5 → 9(3) → 10 → 6
|
解説の数字の選び方はあくまで一例です。順番が違っても勝てる手順もあります。改めて番組を見返すと、東大生チームが後手を選択したときに先手の中村先生が「え〜〜」と言いながらメモを見ていましたが、この時は先手が「4」を選ぶ方法を使い中村先生は勝ちました。
というわけで、やはり必勝法には強かった。コマ大フィールズ賞はマス・ポヌペア。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年7月
「結び目理論(7/27)」
東大生チームは杉山・瀬戸山ペア。研究生が続々登場する中、正解を出して意地を見せたいところです。
問題:
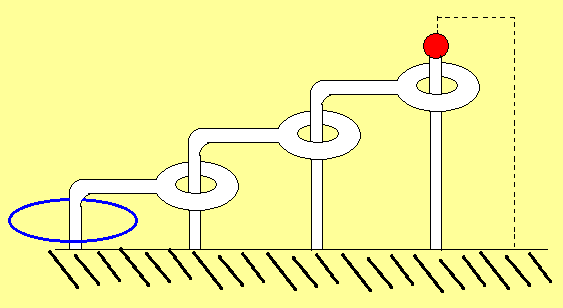
図のような状態から紐(青)を離すには、紐が点線部分を最低何回通る必要があるか。
紐は伸縮自在でどんな長さにも伸び縮みができるものとする(下の斜線部分は台座であり、ここを
紐が通ることはできない)
|
今回の問題は、早稲田大学の吉川先生から提供された。コマ大チームは少しでもヒントをもらうためにその吉川先生の研究室を訪れた。研究室の学生は今回の問題のような紐がかかったパズルを解きながら研究を進めている。
ひとしきり「結び目理論」の話を伺ったところで、今回の問題のヒントをもらうために少し小さい形のパズルを解くことにした。しかしそのパズルを大きく作ったためにコマ大メンバーは紐を持って行ったり来たり…その解答を元に、今回の問題の正解を導き出す。
|
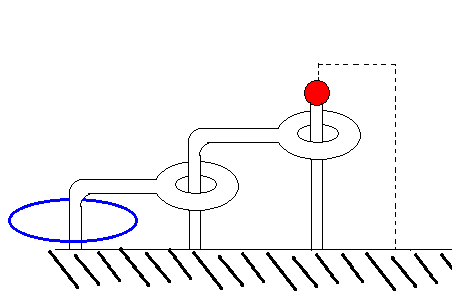
これが少し小さいパズル
|
マス・ポヌペアと東大生チームにもコマ大が使った少し小さい形のパズルが用意された。机の上で紐を動かしているうちにスルリと紐が抜ける。しかしそれで喜んではいけない。問題のパズルは一回り大きいため、どのように解くかを考えなければいけない。刻一刻と時間が過ぎる。
| コマ大チーム | 6回 | 小さい物から2回、4回で解けたことから |
| マス・ポヌペア | 16回 | 小さい物から2回、4回で解けたことから |
| 東大生チーム | 8回 | 小さい物から2回、4回で解けたことから |
3組とも一回り、二回り小さい形のパズルで、紐が解けるまでの回数は一致しているが、そこから正解の求め方で別れた。東大生チームは実証したというが、果たして合っているのか?
正解…8回 東大生チーム正解!!
「論より証拠」の勝利。見事に東大生チームが正解を出した。これは小さいパズルから順番に考えていく。まず、一番小さいパズルは次のもの。
この場合は2回で紐が解ける。続いてその次の大きさのパズルの場合…
2回紐を動かしたら、紐が真ん中の棒にかかる状態に変わった。これは先ほどの一番小さいパズルの形である。つまりあと2回で紐が解けるため、回数は4回。
そして、この次の大きさのパズルが今回の問題のパズル。
こちらは4回動かすと紐の状態は下の真ん中のような形になるが、この紐を動かすと、左から2番目の棒に紐がかかっている状態になる。これはひとつ前のパズルの状態になるため、あと4回紐を動かせばひもが解ける。よって移動する回数は8回となる。私は「10回」になってしまった。なんでだろうか??勿論コマ大フィールズ賞は東大生チーム。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年7月
