数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年9月
「コマ大数学科」に挑む・12年9月
最終更新日2012年11月3日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「ジョルダン曲線 (9/7)」
東京での放送は8月だったコマ大。夏休みの自由研究について東大生チーム木村さんは「変わった野菜を集める」瀬戸山さんは「おいしいチャーハンの作り方」と回答。ちなみに私は…何したっけ?
問題:
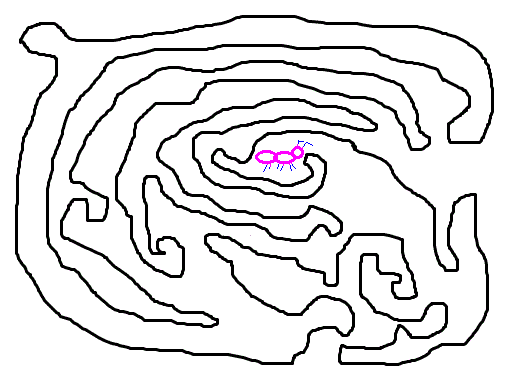
図の中のアリは曲線の内側、外側のどちらにいるでしょうか?
|
シンプルな問題。アリの道をたどれば分かる。だがコマ大チームは一味違う。実際に小動物を使って検証を行う。ロープで問題の曲線を作り、その中に動物を入れて外に出ることができるか見守る。まず本物のアリを使ったが、ロープを軽々と超えてどこかに逃げてしまった。そのあともハムスター、カブトムシを使ったが答えが出ず。最後のカメに託したが、歩みがのろいため撮影時間が終了。一応カメが外に出るかじっと見守った。
今回は全部で問題が3問ある。早く確実な方法で答えを出せるかどうか?残り2問はこちら。
問題2:
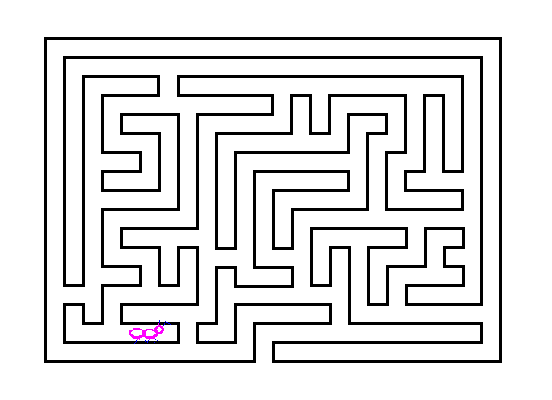
図の中のアリは曲線の内側、外側のどちらにいるでしょうか?
|
問題3:

図の中のアリは曲線の内側、外側のどちらにいるでしょうか?
(放送では目と口が浮き出て顔のような形になるのですが、私の画力では限界でした。
色づけでごまかしています。色は何の関係もありません)
|
マスも東大生も最初の問題には時間がかかったが、コツをつかんで、3問目にはまさに秒殺となった。
コマ大チームは1問目はカメに頼ったが2,3問目は自力で答えを出した。
各問題の解答は以下の通り。
| コマ大チーム | 第1問:外、第2問:外、第3問:内 |
| マス・ポヌペア | 第1問:内、第2問:外、第3問:内 |
| 東大生チーム | 第1問:内、第2問:外、第3問:内 |
1問目だけコマ大チームは違った解答。はたしてカメの歩みは正解を導いたのでしょうか?
正解…第1問:内、第2問:外、第3問:内 マス・ポヌペア、東大生チーム正解
見事2組が全問正解を果たした。答えを導く方法はこちら。
|
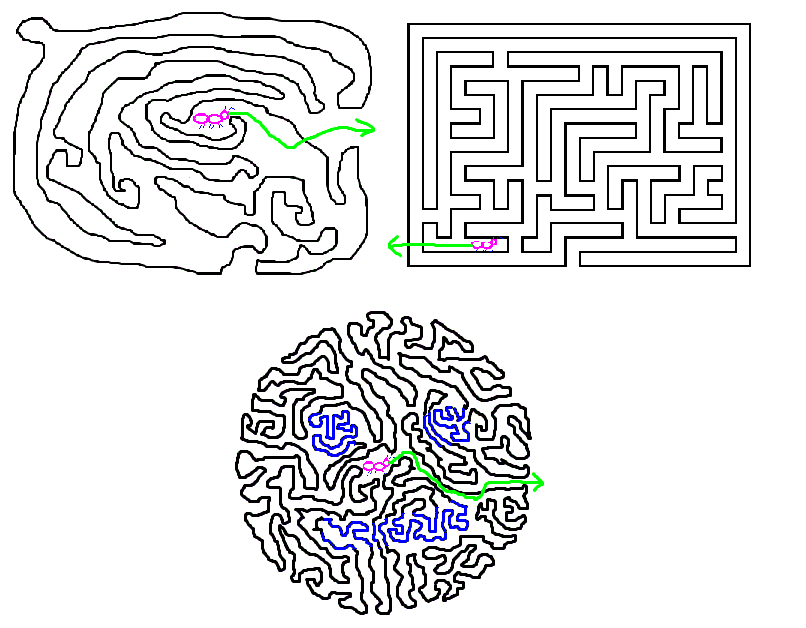
曲線のある地点から外へ向かう道を考える。このとき壁を乗り越える道でも構わない。このとき閉じた
曲線であれば、奇数回壁を越えたら「内側」偶数回壁を越えたら「外側」にいることが分かる。
今回の3問について図のように外へ向かう道を考えると、1問目は1回、2問目は2回、3問目は1回壁を越えているため、順に「内」「外」「内」にアリがいることが分かる。
|
小学生でも調べることができるこの判定法。実は数学的な証明は議論が始まってから100年以上も後のこと。全問正解のマス・ポヌペアと東大生チーム。マスの「レディーファースト」の一言でコマ大フィールズ賞は東大生チームに。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年9月
「ランダムウォーク (9/14)」
今回はひたすら歩く問題?
問題:
8×8の格子状に並んだ点があります。図の点Aからスタートさせて上下左右の隣の点に移動する
プログラムをコンピューターに入力しました。このとき移動する点は15回曲がって、
最後は突き当たって止まりました。
このとき、点の移動の最長距離とその軌道を求めなさい。ただし、同じ軌道を2回以上通ることは
できません(同じ点を2回以上通ることは可能です)

|
コマ大の検証はまさに「ランダム」床に並んだ点を移動して長い距離を探し出す。そこで登場したのは気まぐれロボット「きたごう」とにかくランダムに、しかし長い距離を求めてひたすら点の上を動く。
マスも東大生チームもとにかく線を引いて考えていく。ある程度長い距離の解答を出して、さらに長い距離を出すか模索をする。さて、どこまで長い距離を出せたのか?
|
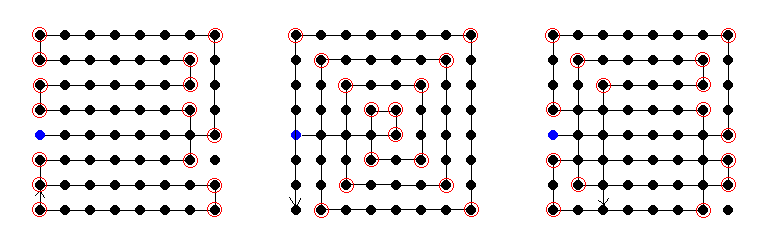
| コマ大チーム | 64(左図) | あえて通らない点を作った。 |
| マス・ポヌペア | 67(中図) | 中央から回転する軌道。 |
| 東大生チーム | 73(右図) | 交差する点を多くとるようにした。 |
|
東大生チームの「73」という解答にコマ大チームもビックリ。はたして正解は出たのでしょうか?
正解…76 全員不正解!
東大生チームの上を行く「76」、さてどのような軌道をたどるのでしょうか?
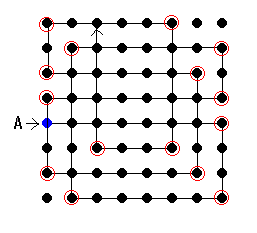
現在分かっている最長距離は「76」しかし、これより長いものがあるのかないのかは分かっていない。もしかしたらこの番組で最長記録が出たかも??今回は残念ながら正解が出せなかったが、最も長い距離の答えを出した東大生チームがコマ大フィールズ賞を取った。ちなみに私は「69」まで見つかった。もう一歩だったかな?
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年9月
「和算 Part 5 (9/21)」
江戸時代の算学者渋川春海を描いた映画「天地明察」が公開される、ということで今回は和算の問題
|
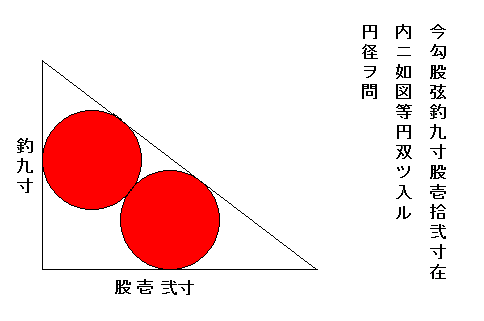
右側の文章は当時の問題文。現代の言葉に替えると以下の通り。
問題:
直角三角形の縦が九寸、横が十二寸である。この直角三角形の同じ大きさの円2個が
図のように入っているとき、この円の直径を求めなさい。
|
神頼みのコマ大チームは神社に向かう。問題の答えを出せるようお参りをして、ついでにほかのお願いもしたところ神のお告げ(?)で受けたヒントは「風船」
ということで、問題の寸法の直角三角形の部屋を作り、中に2個の風船を入れる。この風船が同じ大きさになるようにふくらまして問題の図のようになったときの寸法を測ってみる。久しぶりの重労働の検証の結果は如何に?
今回東大生チームの研究生はフラダンスサークルに所属する淡路さん。ここしばらくの東大生チームの強さをキープするかのように計算を進めていく。同じくマス・ポヌペアも着実に計算をしていく。答えが出そろいました。
| コマ大チーム | 4.5寸 | 検証の結果 |
| マス・ポヌペア | 4.6寸 | 2等分線を引いて計算 |
| 東大生チーム | 7分の30寸 | 相似を使って |
ほぼ近い値がそろいました。正解はあるのでしょうか?
正解 … 7分の30寸 東大生チーム正解
見事東大生チームがご明察(=正解)今回の問題は中学生でも頑張れば解ける内容であった。まず斜辺の長さが15寸になることは分かると思います。それを頭に入れて解説。
番組では木村さんの解答の説明がなかったですが、おそらく以下のような計算だと思います。
この解答はマスがひらめきそうな感じがします。とはいえコマ大フィールズ賞は勿論東大生チーム。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年9月
「視聴者からの挑戦状 Part 5(9/28)」
今回の問題を出題をした視聴者はこのシリーズ初の女性。果たしてどのような問題か?
問題:
以下のルールに従ってボールを避けるゲームを行う。
- 一発ずつ投げられてくるボールを避ける。
- ボールが当たる確率は1/2。
- 一度ボールが当たった場合、次にボールが当たる
確率は5/8になる。次のボールを避けると、次にボールが当たる確率は1/2に戻る。
- ボールが続けて2回当たるとゲームは終了。
このとき、5発目までゲームが続き、5発目にボールを避けられる
確率を求めなさい。
|
コマ大チームは実際にボールに当たりながら…いや、避けながら検証。訪れたのはとある小学校。ここにはドッジボールの強豪チームがある。そのチームのメンバーの選抜8人から一人を選び、コマ大チームに向かってボールを投げる。飛んでくるボールが当たるかどうかは問題のルールに従っている。
相手は小学生とはいえ、やはりボールが当たると痛い。アラフォーメンバーのコマ大チームは見事ボールに当たる…いや、避けることができるのか?
ここしばらくコマ大フィールズ賞を受けている東大生チーム。今回は杉山・瀬戸山ペア息の合った連係プレー…と思ったら、別々の計算をしていた。でも最後に確認を済ませて解答。マスも負けてはいないがここしばらく東大生に一歩及ばず。答えを導き出せるか?
| コマ大チーム | 1/4 | 検証の結果。コマ大チーム4人で
ダンカン部長のみ成功したため |
| マス・ポヌペア | ずらずらと計算が
並んだ解答 | 当たる、当たらないの順番を書き出して計算…
しかし、時間に間に合わず |
| 東大生チーム | 91/512 | 樹形図と漸化式を使って計算 |
コマ大チームはダンカン部長が成功したが、これもかなりルールを変更した結果。計算で出した東大生チームの解答は正解か?
正解…91/512 東大生チーム正解!!
東大生チーム、お見事!!ちなみに私は樹形図を使ったがいくつか書き忘れて「79/512」という解答。まあ、私は置いといて解説です。
漸化式を使った解答は以下の通りです。
問答無用の解答で東大生チームはコマ大フィールズ賞を取った。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・12年9月

