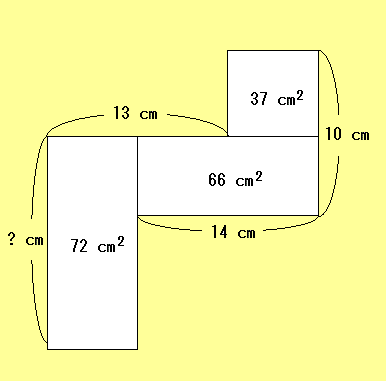
問題：３個の長方形が図のように並べています。面積と長さが図のように分かっているとき、左端の「？」の値を求めなさい。ただし、計算の途中で分数を使ってはならない。
「コマ大数学科」に挑む・１２年１２月
最終更新日２０１３年１月３０日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| Ex3 パズル(12/7) |
| 入社試験に挑戦(12/14) |
| 外資系入社試験(12/21) |
| 線が千(12/28) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
問題： ３個の長方形が図のように並べています。面積と長さが図のように分かっているとき、左端の「？」の値を求めなさい。ただし、計算の途中で分数を使ってはならない。 |
|
140 cm^2 - 37 cm^2 - 66 cm^2 = 37 cm^2 この面積は青の長方形の面積である。青の長方形と右隣りの長方形は面積も同じで、高さも同じ。つまり横の長さも同じである。このことから青の長方形の横の長さは 7cm である。 このことから左の長方形の横の長さが 13 cm - 7 cm = 6 cm となるため、高さは 72 / 6 = 12 cm これが求める長さである。 |
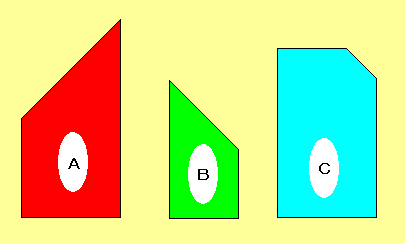第１問：右の図のＡとＢを使い、線対称の図形を作りなさい。第２問：右の図のＢとＣを使い、線対称の図形を作りなさい。 第３問：右の図のＡ，Ｂ，Ｃを使い、線対称の図形を作りなさい。 いずれの問題でも図形を重ねてはいけない。また、各図形は裏返して 使ってもよい。 |
第１問 ３組が一斉に答えを出した。とりあえず１位：コマ大チーム、２位：東大生チーム、３位：マス・松本ペアとなった。
第２問 こちらも３組が一斉に答えを出した。今回は１位：東大生チーム、２位：マス・松本ペア、３位：コマ大チームとなった。
|
|
|
|
私は１問目は分かりましたが、２問目はテレビの速さに負けて答えを出せず。３問目は答えを出せなかった…というか、ここで答えを知りたくはなかった。解けるまで悩みたかった。
世界を魅了するパズルは、さすがに世界の北野には勝てなかったのか。コマ大フィールズ賞はマス・松本ペア。
数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１２年１２月
「入社試験に挑戦 (12/14)」
|
１問目： Ａ，Ｂ，Ｃ，Ｄ，Ｅの５人が同じマラソンコースでマラソン競争を行いました。走り終わり、５人は以下のコメントを残しました。
Ａ「ＣにもＤにも負けてしまいました。」 ５人のコメントのうち、１人だけうそのコメントを言っています。このとき、実際３位に入った人は誰でしょう。 １．Ａ ２．Ｂ ３．Ｃ ４．Ｄ ５．Ｅ |
今回のポヌさんの代役は東大生のフラガール淡路さん。レギュラーの東大生チームも負けてはいない。問題をあっという間に解いてしまった。と、いうわけで今回は問題がもう１問ある。
|
２問目： 図のような立方体Ａと直方体Ｂが各１５個あります。これらのうち何個かを使い、図のような大きな立方体を作りました。このとき使われなかった立方体Ａは最大何個になるでしょう。
１．9 個 ２．10 個 ３．11 個 ４．12 個 ５．13 個 |
| １問目 | コマ大チーム：４ | 東大生チーム：４ | マス・淡路ペア：４ |
| ２問目 | コマ大チーム：２ | 東大生チーム：２ | マス・淡路ペア：３ |
|
１問目：５人のコメント内の順位を不等号で表す。「大なり」の方を上位とする。
Ａ：Ｃ＞Ａ，Ｄ＞Ａ
青字のコメントは同じ結果である。この結果がウソであれば、ＢとＤの２人がウソをついたことになるが、実際は１人しかウソをついていない。つまり青字のコメントは正しい結果である。 Ａのコメント「Ｃ＞Ａ」がウソであれば「Ａ＞Ｃ」が正しい結果になる。このとき「Ａ＞Ｂ」となるため、Ｂの２番目のコメントもウソになり２人がウソをついたことになる。このことから「Ｃ＞Ａ」は正しい結果である。 この時点でＣはＡ，Ｂ，Ｄより上位であることが分かるため必ず２位以内である。つまりＣの２番目のコメントがウソであることが分かる。他のコメントの組み合わせると順位は「Ｅ＞Ｃ＞Ｄ＞Ｂ＞Ａ」となり、３位に入ったのは「４．Ｄ」である。 |
|
この部分をＢだけで作ろうとするとできないことが分かる。しかしＡを２個、Ｂを２個では作ることができる（Ａを１個だけはできない） つまり、この立方体を作るために必要な立方体Ａは、問題で見えていた３個と見えていない部分２個の合わせて５個は最低でも必要である。よって使われない立方体Ａは最大 15 - 10 = 5 個（つまり２．）である。 |
数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１２年１２月
「外資系入社試験 (12/21)」
|
問題： あなたはある組織にとらわれて、以下のゲームに挑むことになりました。
・白の玉１０個と黒の玉１０個が与えられている。 以上の条件のとき、釈放される確率が最も高くなるのは何％で、どのように玉を振り分けたときでしょう？ |
今回の問題をいかに解くか…と思われたが、マスも東大生もあっという間に解いてしまった。解答は以下の通り。
| コマ大チーム | １００％ | 一方に白玉１個、残りをもう一つの箱へ あとは誘導作戦で白玉だけの箱へ？ |
| 東大生チーム | ７３．７％ | 一方に白玉１個、残りをもう一つの箱へ |
| マス・ポヌペア | ７３．７％ | 一方に白玉１個、残りをもう一つの箱へ |
正解… 73.7% 東大生チーム、マス・ポヌペア正解
|
一つの箱に白の玉 a 個、黒の玉 b 個が入っているとき、この箱から白の玉が選ばれる確率は a/(a+b)
である。この確率が 50% つまり 1/2 を超えるときを考えると
a/(a+b) > 1/2 ⇒ a > b つまり白の玉が黒の玉より多いときである。一方確率が 1/2 より低いときは a < b、つまり白の玉が黒の玉より少ないときである。 |
|
問題のゲームについてボスが箱を選ぶ確率を 1/2 とすると、２つの箱とも白・黒５個ずつ玉を入れれば、釈放される確率は 1/2 である。
釈放される確率を 1/2 より高くするためには、少なくとも一つの箱の確率を 1/2 より高くしなければならない。つまりこの箱には白の玉が多く入っている。 |
|
白の玉が多く入っている箱で釈放される確率を最も高くするためには、黒の玉が入っていない時が確率 1（100%）である。 一方、黒の玉が多く入っている箱で釈放される確率を最も高くするためには、白の玉９個、黒の玉１０個入っているときである。 これら２つの箱の玉の状態に振り分けることができるため、全体の確率は 1/2 × (1 + 9/19) = 14/19 （およそ 73.7%）である。 |
数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１２年１２月
「線が千 (12/28)」
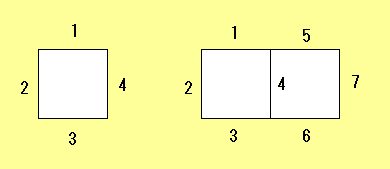問題：１ｃｍの線分を４本使って一辺が１ｃｍの正方形が１つできます。 ７本を使うと一辺が１ｃｍの正方形が２つできます。 では１ｃｍの線分を１０００本使うと、一辺が１ｃｍの正方形が最も多くて何個できるでしょう？ |
今回は計算勝負。東大生はもちろん、マスもしっかりと計算をして答えを探す。解答は以下の通りとなった。
| コマ大チーム | ４７８個 | 検証の結果 |
| 東大生チーム | ４７８個 | まず正方形を作って、余りの線分で正方形を作る |
| マス・ポヌペア | ４９９個？ ４８１個？ | 東大生チームとほぼ同じ計算だったが… |
正解…４７８個 コマ大チーム、東大生チーム正解！！
今回は着実に計算を進めると答えが出てきます。まず、なるべく多くの正方形を作るためには、線分で作る図形はひとつながりで穴やくぼみがない図形でなければいけません。そうするとなるべく正方形に近い図形である必要があるわけです。それ以降の計算は…
|
一辺が n 本の線分からなる正方形（n^2 個の正方形）を作るために必要な線分は
n × (n+1) × 2 = 2 n^2 + 2 n 本 1000 本の線分でなるべく大きい正方形を作るためには、2 n^2 + 2 n ≦ 1000 ≦ 2(n+1)^2 + 2(n+1) という式を考えればよい。n = 21 のとき
2 n^2 + 2 n = 924 ≦ 1000
大きい正方形の一辺に沿って21個の正方形を作る…線分は 2×21 + 1 = 43 本。 21^2 + 21 + 16 = 478 個
|
数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１２年１２月
