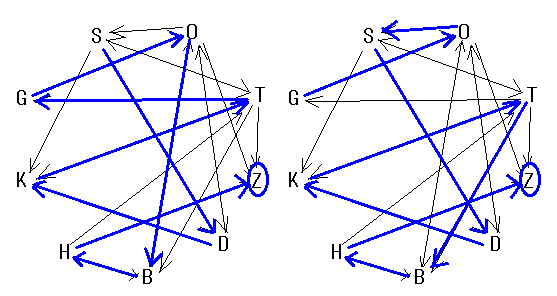
次に一つの文字に向かう正解の矢印は2個以上ないことから「D→K」「B→H」「S→D」「H→Z」の矢印が使われることが分かる。
この時点で「S→D→K→T」「G→O」「B→H→Z」の3つのルートが使われることが分かる。「S」「G」のいずれかで始まる場合を考えると、どちらの場合でも問題の条件を満たすルートが作ることができる。
「コマ大数学科」に挑む・13年2月
最終更新日2013年3月24日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 外資系企業に挑戦 Part 2(2/1) |
| The Playful Brain(2/8) |
| 主成分分析(2/15) |
| 逃亡者(2/22) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「外資系企業に挑戦 Part 2 (2/1)」
問題:4人の探検家が暗い山道を歩いていると細くて崩れそうな橋を見つけました。
4人はこの橋を渡りたいのですが……
|
コマ大チームの検証は問題の通りに最短時間を探すことに。しかし橋は渡らず、箱根駅伝をモデルに10か所の地点を通る往復区間を走る(?)Aが一人で走るときは1歩1秒で10歩が10秒。一方Dが走るときは1歩が10秒、10歩を100秒かけてゆっくりと進む。寒い中で速く、ときにゆっくり進みながら答えを出した。
2組は意外にすんなりと解答を出した模様。マスは石井さんに新ネタを伝授(?)東大生チームは新ネタを伝授しながらも「もっと早くなるのでは」を試行錯誤を繰り返す。これが思わぬ解答を生み出した。
| コマ大チーム | 170秒 | 検証の結果 |
| マス・ポヌペア | 170秒 | CとD2人で橋を渡らせる。 |
| 東大生チーム | 130秒 | まずCとD2人で橋を渡らせる。 そのあとCとDが懐中電灯で誘導させて A,Bを渡らせる。 |
正解…170秒 コマ大チーム、マス・ポヌペア正解!!
東大生チームの作戦は見事に失敗。解説で中村先生が「もっと短くなると思い3日悩んだ」と話したが、CとD2人を渡らせる方法を見つけると、以下の考え方で170秒が最短になることが分かる。
|
橋を渡る方法として以下の手順で行う(多分ほかに方法はないはず)
2人が渡る→1人が帰る(向こうに1人残る)→2人が渡る ここで注意することは ・2人で渡るときは遅い人に合わせるため、必ず20秒以上かかる。 ということである。 もしC、Dがそれぞれ別に渡ったとしたら、2人が渡る3回のうち2回は50秒、100秒かかり、残りの1回は最低でも20秒。帰る2回は最低でも10秒かかるためこの方法で渡りきる最短の時間は 50+100+20+10+10=190秒 |
|
一方CとDが2人一緒に渡るとしたら、2人が渡る3回のうち1回は100秒かかり、残りの2回は最低でも20秒。帰る2回は最低でも10秒かかるためこの方法で渡りきる最短の時間は
100+20+20+10+10=160秒 しかし渡るときの時間が100秒、20秒、20秒であり、帰るときの時間が10秒、10秒となる渡り方は作ることができない。160秒の次に短い170秒は渡るときの時間が100秒、20秒、20秒であり、帰るときの時間が10秒、20秒となる。この条件を満たす渡り方は以下の2通りがある。
A,Bが渡る(20秒)→Aが帰る(10秒)→C,Dが渡る(100秒)
A,Bが渡る(20秒)→Bが帰る(20秒)→C,Dが渡る(100秒) したがって、190秒より短い170秒で渡る方法があり、この方法が最短である。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年2月
「The Playful Brain (2/8)」
|
問題:以下の9個の映画のタイトルを最初のアルファベットが次のタイトルに含まれるように並び替えなさい。
|
全員同じ答えが出た。
|
SONATINE → DOLLS → KIDS RETURN → TAKESHIS → GETTING ANY? → OUTRAGE BEYOND → BROTHER → HANA-BI → ZATOICHI |
|
GETTING ANY? → OUTRAGE BEYOND → SONATINE → DOLLS → KIDS RETURN → TAKESHIS → BROTHER → HANA-BI → ZATOICHI |
|
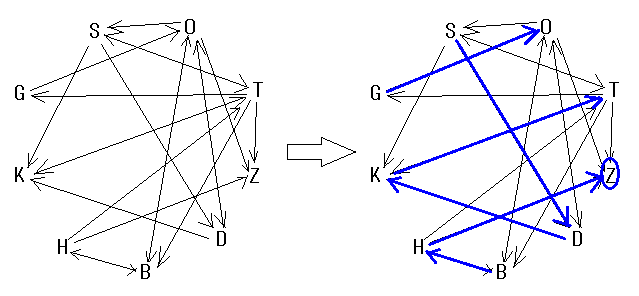
9個の最初のアルファベットが、どの映画のタイトルに入っているかを矢印で表すと下の図の左の通りにある。図では映画のタイトルの最初の文字のみを表示。たとえば「S」は「SONATINE」を表し、
「D(DOLLS)」は「S」が含まれているため「S」から「D」に矢印が出ている。
次に一つの文字に向かう正解の矢印は2個以上ないことから「D→K」「B→H」「S→D」「H→Z」の矢印が使われることが分かる。 この時点で「S→D→K→T」「G→O」「B→H→Z」の3つのルートが使われることが分かる。「S」「G」のいずれかで始まる場合を考えると、どちらの場合でも問題の条件を満たすルートが作ることができる。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年2月
「主成分分析 (2/15)」
|
問題:
図のような3つの位置にそれぞれ1軒ずつ家が建っています。ここに道路を一本作るとき、以下の条件を満たす道路はどのようにできるか見つけなさい。
・道路から各家までの建設費用(道路までの最短距離)の合計は最小に抑える。 |
問題を見てマスは一言「幅の広い道路を一本」すかさず中村先生が「道路は幅のない直線」と釘を指す。マスは三角形を描いて、円を描いて…と作図をすすめる。東大生チームはなが〜〜い式を書いていく。先に正解を出すのはどちらか?
| コマ大チーム | 距離の合計1.4m | 青と緑の家をむすんだ直線 |
| マス・ポヌペア | 作図を表示 | 三角形の2辺の中点を 通る直線。 |
| 東大生チーム | 5/√13 | 青と緑の家をむすんだ直線 |
正解…青と緑の家を通る直線、距離は5/√13 東大生チーム正解!
コマ大チームも直線を求めたため正解。マス北野は「家を通る道路を作るなんてひどいだろ!!」と猛抗議。解説の中村先生もさすがにタジタジであった。何はともあれ解説。
|
平行な直線の中で距離の合計が最小になるものは、3点のうち1点を通り、3点からなる三角形を横切る( or 三角形の辺となる)直線である。図の黒の矢印が指す直線がその直線。
直線が3点の外にあるとき、3点に近づくように直線を平行移動させると3点との距離は短くなる( 図の青の線が短くなる距離)ため、距離の合計は小さくなる。 さらに直線を三角形を横切る方向に平行移動させると、1点は距離(赤の線)が長くなり、2点は距離(緑の線)が短くなる。よって距離の合計はさらに小さくなる。距離の合計は三角形を横切り、1点を通るところで最小になる。 |
|
1点を通る直線で傾きを変えていくと、3点の距離の合計が短くなるのは2点を通る直線になった時である。図の黒の矢印が指す直線がその直線。
上の図のように1点を通る直線と、2点を通る直線について3点の距離を比べる。このとき2点を通る直線が赤の線の距離がなくなり、青の線が緑の線の距離に変わる。 青の線が緑の線に変わると距離は長くなるが、赤の線の距離がより長いため、3点の距離の合計はより短くなる。 |
|
以上から3点のうち2点を通る直線と残り1点との距離を調べて、その中で最小の距離が求める直線と距離であることが分かる。 3点からなる三角形を考えたとき、この距離は三角形の「高さ」に、直線上の2点の距離は「底辺」にあたる。三角形の面積は変わらないため「底辺」が長いほど「高さ」は短くなる。 三角形の面積と各辺の長さを求めると、
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年2月
「逃亡者(2/22)」
|
問題:あなたは円の形をした池の中央でボートに乗っています。池の岸にはハンターがおり、彼から逃げなければいけません。以下の条件のときハンターに捕まらずに岸までたどり着けられる方法を考えなさい。
・ハンターはボートの速さの4倍の速さで岸を走ることができる(池の中には入れない)
|
マスも東大生チームも螺旋を描くような逃げ方を考えている模様である。そんなとき東大生チーム木村さんが何やら思いついて、菊川さんも思わずニッコリ。さて何を思いついたのか?
|
| |
| コマ大チーム | 少し方向を変えて、ハンターが動いたところで反対方向に曲がりながら進む |
| マス・ポヌペア | ハンターに背を向けるように進みながら、途中で方向を変えまっすぐ岸に進む |
| 東大生チーム | 螺旋を描くように岸に向かう |
判定…全員不正解!
竹内先生が示した解答は「逃亡者」と「ハンター」に似つかわしくない、何とも地道な方法である。
|
その地点から池の中心を中心とする円に沿って移動する。この移動に合わせてハンターは追いかけるが、 池の半径の1/4の少し手前であるため、ハンターはあなたから最短の位置の岸には追いつけない。つまり少しずつハンターから離れていく。 このまま動き続けると、ある地点でハンターと池の中心を挟んで反対の位置に来ることができる。この時点で岸に向かって進むとハンターは追いつけずに逃げることができる。 |
|
岸にまっすぐ向かいハンターから逃げ切るために必要な岸からの距離は、ハンターが進む池の半周分の4分の1でなければならない。
池の半周の長さは約 3.14 となるため 3/4 + α < 3.14/4 ⇒ α < 0.035 となる。 |
| 例えば池の半径が 10 mのとき、ハンターから逃げ切るためには、まず池の中心から 10 × (1/4 - 0.034) = 2.16 m の位置で回り続ける。そしてハンターと池の中心を挟んで反対の位置に来た時に岸に向かって 7.84 m まっすぐ進むとハンターから逃げ切れる…といってもハンターとの差はわずか数cmである。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年2月