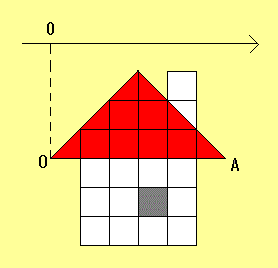
図の図形を糸でつるして線分ACが水平になるようにしたい。糸でつるす場所は 0 から何センチの位置になるか?
図の四角は一辺が1cmの正方形である。灰色の正方形は穴が空いている。赤と白の色分けは重さとは関係がない。念のため…
「コマ大数学科」に挑む・13年3月
最終更新日2013年4月29日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| モビール(3/1) |
| テラガ・ブルク(3/8) |
| ボウリング(3/15) |
| プラスとマイナス(3/22) |
| 最大円柱(3/29) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
問題: 図の図形を糸でつるして線分ACが水平になるようにしたい。糸でつるす場所は 0 から何センチの位置になるか? 図の四角は一辺が1cmの正方形である。灰色の正方形は穴が空いている。赤と白の色分けは重さとは関係がない。念のため…
|
| コマ大チーム | 3.3cm | サザエさんの家に似ていることから 「サザエ→3.3 A」と決定? |
| マス・ポヌペア | 3.75cm位 | 重心を計算 |
| 東大生チーム | 3.15cm | 面積が半分になる位置を計算 |
|
重さが M1, M2 の物の重心の位置が基準点 0 からそれぞれ v1, v2 の位置にあるとする。
また、2個の物を合わせた物の重心の位置が基準点 0 から v の位置にあるとする。このとき
以下の式が成り立つ。
v × (M1 + M2) = v1×M1 + v2×M2
また、k 個の物を合わせた物の重心の位置が基準点 0 から v の位置にあるとする。このとき 以下の式が成り立つ。 v × (M1 + … + Mk) = v1×M1 + … + vk×Mk |
|
・重さの合計:M1+M2+ … +M5 = 43/2 となるため、問題の図形の重心の位置は 11/6 × 2/43 = 11/129 しかし、問題では基準の 0 の位置がずれていたため、ずれた距離 3 を加える。11/129 + 3 = 398/129 ≒ 3.085 この値が釣り合う位置になる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年3月
「テラガ・ブルク(3/8)」
|
問題:下の図の状態から2人が緑が先手、赤が後手でゲームを行う。互いに一個のコマを別の丸の位置に線に沿って移動させていく。他のコマを飛び越えて動かすこともできない。また他のコマと重ねることもできない。
相手を動かせない状態にしたら勝ちである。 このゲームの戦法とゲームが終わるまでの最低手数を求めなさい。
|
コマ大チームと同じく、実際にコマを動かしながら必勝法を探す2組。私もノートに何個も図を描いて考えているが、これという必勝法は見つからず。どうやら2組も同じように悩んでいる。
|
| |
| コマ大チーム | 6手で勝敗が付く。先手が「必敗」? |
| マス・ポヌペア | 6手で勝敗が付く。実戦での結果 |
| 東大生チーム | 6手で勝敗が付く。5手目でミスを すれば、という条件 |
|
3手までは以下の手順でしかない(左右反転も含む)
|
|
|
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年3月
「ボウリング(3/15)」
|
問題:ボウリングでストライクを8回出して、しかもガターを一回も出さないのに得点が100点未満となりました。 このときのスコアを求めなさい。 ストライク、スペアを取ったフレームの得点は以下の通り。
ストライクを取った場合:10点+その後の2投の得点がそのフレームの得点
|
オープニングでボウリングはからっきし駄目と話していた東大生瀬戸山さん。しかし問題をあっさり解いてしまった。マスもしっかり確認してから正解を導いた。ちなみに私はずっと悩んでいた。答えは出せず。今回は見事に正解がそろった。
| コマ大チーム | 99点 | プロボウラー鈴木さんが登場し 解答のスコアを実際に出した。 |
| マス・ポヌペア | 99点 | 2連続ストライクを動かすと 何通りかできるかも、と一言 |
| 東大生チーム | 99点 | 9フレームはストライクにならない 所から考えた |
正解はもちろん99点で全員正解。ある程度見当を付けて答えを出すこともできるが、理論的に100点未満の投げ方を絞り込むことができる。
|
ストライクを1回以上続けてとった時の点数を調べると
|
|
1〜9フレームと10フレームの3投の合計12個の中にストライク8個を並べると、残りの4個分はストライク以外になる。 もし10フレームの3投目がストライクでないとすると、残りの11個にストライク8個を並べることになる。4連続以上のストライクを取らないように並べるには
・3連続ストライク2回+連続しないストライク2回 |
|
10フレームの3投目でストライクを取るためには「2投目でスペアを取る」または「3連続ストライク」のいずれかでなければならない。
|
|
9フレームもストライクを取ると、9,10フレームで合計60点取る。残りストライクが4個残っているため、必ず100点以上になる。したがって9フレームはストライクを取れない。1〜8フレームでストライク5個を並べると、
2連続ストライク1回+連続しないストライク3回 という構成でなければ100点以上になる。これらの順番を調べると、いずれの場合でも最終スコアは99点に抑えられることがわかる。
|
|
ストライクを取るフレームは普通に投げれば(?)大丈夫だが、ストライクを取れないフレームで実際にガターなしで1点のみを取れるか考える。 1投目に左右両端のうち一本を倒す。そのあと2投目は倒したピンのところを通るように投げればガターにならずに済む。 この結果問題の条件を満たし、99点を取ることができる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年3月
「プラスとマイナス(3/22)」
|
問題:下の数字の表のうち縦の列、横の列いずれも3個ずつになるように数字をいくつか選び出し、それらの数字にマイナスを付けます。 このとき、すべての数字の合計はいくつになるでしょう?
|
残ったお茶はすべてブレンド。東大生も飲んだが悪くはないみたい。問題を解くためには適当に数字を選んで計算すれば出てくるが、その解答を理論的に求めるにはどうすればよいのか。先ほどのブレンド茶の効果なのか東大生チームは着実に計算をする。一方今回1人で挑むマス北野。黙々と計算を進める。
| コマ大チーム | 569 | 検証の結果 |
| マス北野 | 520 | 数字全部の合計の1/4になる |
| 東大生チーム | 520 | 数字全部の合計の1/4になる |
正解…520 マス北野、東大生チーム正解!
2組見事に正解。ちなみに私も一応正解。マスも東大生も「プラスの数が全体の5/8、マイナスの数が全体の3/8」として考えた。では、なぜそうなるのでしょうか?
|
例えば上の表で「49」に丸がついているが、2つの表では「48」と「1」に分かれている このため、表全体の数の合計は2つの表のそれぞれの数の合計を合わせたものになる。 |
|
よって1番目の表の数の合計は 0×2 + 8×2 + … + 56×2 = 8×(0 + 1 + … + 7) ×2 = 448 |
|
よって2番目の表の数の合計は 1×2 + 2×2 + … + 8×2 = (1 + 2 + … + 8) ×2 = 72 以上から表全体の数字の合計は 488 + 72 = 520 である。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年3月
「最大円柱(3/29)」
|
問題:底面の半径が10cm、高さが20cmの円錐があります。この円錐に内接する円柱で体積が最大のものの底面の半径を求めなさい。
|
マスと東大生チームが鉛筆を走らせている、その横でコマ大チームが湯呑に水を入れて水の量をはかっていく。この問題、普通に計算していけば答えを出すことができる。しかし、中村先生は「もっと簡単に答えを出す方法がある」とのこと。早々と答えを出した東大生チーム。別解答を出すことができるのか?
| コマ大チーム | 4.2 cm | 検証の結果。ダンカン部長の作った 湯呑が水の量が多かった。 |
| マス北野 | 分かりません! | 体積を
x の関数で表したものの そこからはさっぱり… |
| 東大生チーム | 20/3 cm | 体積を
x の関数で表し、 そこから微分を使い計算。 |
正解…20/3 cm 東大生チーム正解!!
東大生チームのように普通に微分をしていくと、体積が最大になるときの半径は求めることができる。
|
|
|
|
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年3月