問題： 12345×23456×34567×45678×56789×98765×87654×76543×65432×54321 の百の位を求めなさい。

　ん〜〜、一の位ならすぐに分かるが、百の位となると……しばらく沈黙し考える。やや力ずくだが答えを出せる方法を使い計算をする。答えは出した…その計算結果を見て、ひらめいた！！「ひらめく」ってこういう事を言うんですね。
　より簡単に答えが出せる方法を使い改めて答えを確認。さっそく電話を掛ける。電話の向こうでは大騒ぎの声。コマ大チームの声であった。「答えは８ですか？」……「正解です！！」これでいいの？本当にコマ大に出られるの？数々の疑問が頭をよぎる中、ダンカン部長からコメントを求められ「ふつつか者ですが、よろしくお願いします」

　まずは上の問題の解説です。　

12345, 98765 をそれぞれ 5 で割ると 2469, 19753 となる。また、23456, 87654 を 2 で割ると 11728, 43827 となる。 　これらの商と、残りの掛け算の数を掛け合わせて、その答えの一の位の数を求める。 これはそれぞれの一の位を掛け合わせると求めることができる。 9 × 8 × 7 × 8 × 9 × 3 × 7 × 3 × 2 × 1 = 4572288 となるため、これらの商と、残りの掛け算の数の一の位の数は 8 である。 　以上から 　 12345 × … × 54321 = （一の位が 8 の数）× 5 × 5 × 2 × 2 = 下三桁が 800 の数 　以上から百の位は 8 である。

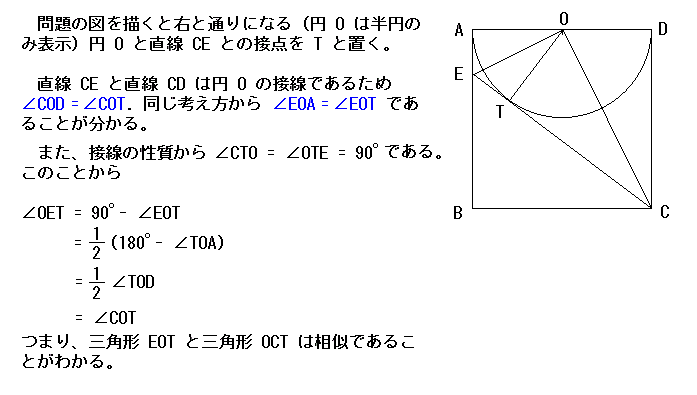
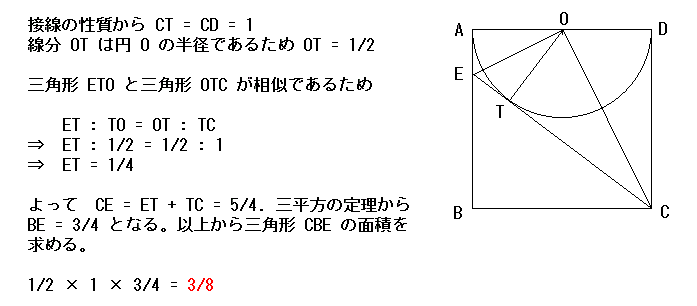
問題： 一辺が１の正方形ＡＢＣＤがある。辺ＡＤを直径とする円の中心をＯ、辺ＡＢ上の点Ｅを直線ＣＥが円Ｏの接線となるようにとる。このとき三角形ＣＢＥの面積を求めなさい。

　今回は「マスマスターグランドチャンピオン大会」として、マスマスターの代表者がスタジオでマス・ポヌペア、東大生チームと対戦する。その前に視聴者からの挑戦状シリーズでおなじみのコマ大チームのラジオ風コーナーが登場。「ビンゴ」の回で行われたコマ大グッズのプレゼントから駒里中学校（略してコマ中）という学校がある話まで様々な話が飛び交った。
　そして「マスマスターグランドチャンピオン大会」の出場者を決める話に進む。事前に問題のメールを送り、解答の電話を待つ。一番手で電話を掛けたのが私。詳しくは上をご覧ください。ということで私の番組参加が決まり、コーナーも楽しく終了。

　ついに私がコマ大に登場…と、その前にちょっと裏話。実はオープニングからコマ大チームのコーナーが流れている間、私はずっと登場するカーテンの後ろで待っていました。ですから、私はあのとき音声だけ聞いていました。改めて、カーテンの奥から私が登場。スポーツ刈りに黒縁メガネの小さい男。あれが私です。３８歳、おっさんです。ダンカン部長とマスの掛け合いの後についに問題が発表。

問題： 定規とコンパスを使い、点Ａ＝４５°を作図しなさい。ただし、コンパスの使用は２回までとする。

　「点Ａ＝４５°」ということだから多分直角二等辺三角形を使うんだろうな、ということは分かる。ただどうやって作ればいいのか？私の周りではコマ大チームが応援をする。解説の竹内先生、そしてタカさんの声も聞こえてくる。結構騒がしい、と思われますが私はそこまで気にはしませんでした。むしろ楽しんでいました。それにしても困ったことに（誰が？）マスも東大生チームも答えが出せない。

　円周角の定理を使うのかな、と考えたときに何となくひらめいた。ダンカン部長が温めていたコンパスをいただき、２回円を描く。そして４５°の角度ができた。私はコマ大チームに半ば無理やり竹内先生のもとに連れて行かれた。判定は…正解。どうしよう。解いちゃった。そしてついに時間切れ。正解者は私一人だけであった。ここでも少し裏話。放送では考える時間が１０分程度になっていますが、実際はもう少し長い時間かかりました。その間私を含め３組とも沈黙。本当に静かな戦いであった。

　私が考えた作図は以下の通り。

1. 点Ａを通る直線を引く。 2. この直線の上にＡ以外の点を一つ決める。 3. 点Ａを通り 2. の点を中心とする円を描く（コンパス１回目） 4. 円と直線の交点で点Ａ以外の点がある。この点を中心にして、2. の点を通る円を描く（コンパス２回目） 5. ２番目の円の直径を一つ決める（番組では２つの円の交点を使いましたが、それ以外の直径でもＯＫです） 6. 直径の両端から 2. の点へ直線を引く。この２直線の交点はタレスの定理より９０°になる。 7. １番目の円と 6. で引いた直線の交点２点から点Ａに直線を引く。この２直線の交点は円周角の定理より４５°になる。

1. 点Ａを通る直線を引く。 2. この直線の上にない点を一つ決める。 3. 点Ａを通らず 2. の点を中心とする円を描く（コンパス１回目） 4. 円と直線の交点のうち、１点と円の中心を結び、直径を引く。円と直線の交点のもう一方の点と直径の一端を結ぶとタレスの定理より９０°が作られる。 5. ９０°をなす交点を中心として点Ａを通る円を描く（コンパス２回目） 6. ９０°をなす２直線と円の交点、そして円の中心で直角二等辺三角形が作られる。この三角形の一頂点である点Ａに４５°の角度が作られる。

　コマ大フィールズ賞は文句なしのコマ大チーム、いや私に渡った。そして瀬戸山さんが学業専念のため出演をしばらくお休み、とのこと。マスから花束を受け取った。

　私のコマ大参加は終了。どうしましょ…勝っちゃいました。こういう時は「あっという間」という言葉を使いますが、私は長く感じました。今回参加、というかお邪魔して思ったことは「番組はこういう風にできるんだ」ということでした。詳しいことは書かないほうが良いと思いますが、番組の構成であったり、人の動きを見ていると勉強になることが多少なりともありました。今回の経験が実生活やこのページなどに生かすことができたら幸いだと思います。

　最後にこの場を借りてお伝えします。

マス北野こと北野武さん、ありがとうございました。
東大生のお二人、ありがとうございました。
コマ大チームはじめ出演者のみなさん、ありがとうございました。
コマ大を生み出している（？）スタッフのみなさん、ありがとうございました

このページをご覧になったみなさん、ありがとうございました。