問題：映画で駅馬車が走っているところを撮影しています。 　駅馬車が一定の速度を超えたとき、馬車の車輪が逆回転しているように 見えました。 　逆回転に見える理由を説明しなさい。

　今回マスのお相手、ポヌさんが公務のためお休み。ポヌさんはベナン共和国全権大使夫人なんですね。コマ大もすごい人達が出てるんですね。それはともかく、マスは一人で問題に挑む。苦戦を強いられる、かと思いきや、しばし考えて早々と解答を書いた。東大生の映画無頓着コンビは逆に苦戦。竹内先生から映画フィルムのコマ数を考えてください、とヒントをもらった。それでも分からず、ついにマスからコマ数のヒントをもらった。

コマ大チーム	目を少し寄らせると 逆回転に見える。	お宮の松の解答。 成田屋のにらみのように？
マス北野	車輪の回転とフィルムのコマが シンクロするため	実際は回転しているが、フィルムは少し逆回転 している位置しか撮影されていない。
東大生チーム	コマ数の限界のため	理論はマスと同じ

正解… マス北野、東大生チームの解説が正解！！

車輪のスポーク（車輪の中心と周囲をつなぐ棒）が８本のものを考える。この時スポークは 45°ずつ車輪に付けられている。 この車輪を回転させて、フィルムで撮ってみる。映画のフィルムが１秒間に２４コマ撮影できるとする。

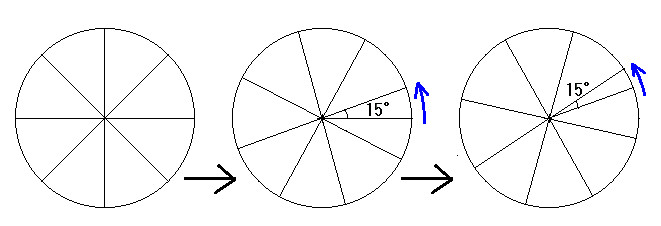
車輪が１秒間に１回転しているとき、フィルムは車輪が 360°/24 = 15°回転するたびに撮影される。このときは、車輪の実際の回転と同じ方向に回転しているように見える。

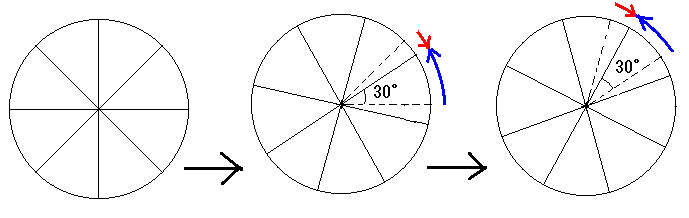
回転を速くして、車輪が１秒間に２回転させる。このときフィルムは車輪が 15°× 2 = 30°回転するたびに撮影される。 　次に撮影される画像は実際には車輪が 30°回転しているが、前の画像の隣のスポークとは 15°しか差がないため、隣のスポークが 15°逆回転して撮影されていると錯覚を起こす（下の図では車輪は青の矢印の回転をしているが、赤の矢印の回転をしていると錯覚する） 　この錯覚が繰り返されているため、車輪が逆回転しているように見えてしまう。

問題： 12345×23456×34567×45678×56789×98765×87654×76543×65432×54321 の百の位を求めなさい。

解説： 　12345×23456 は一の位が 0 になる。つまりこの掛け算の積は 10 の倍数。同様に 98765×87654 も 10 の倍数である。 　よって問題の計算式は 10×10 = 100 の倍数、つまり下二桁は 00 である。

このことから問題の計算式の百の位は計算式を 100 で割った値の一の位になる。 ここで計算式全体を 100 で割らずに上の説明の２つの掛け算それぞれを 10 で割った値 と残り６個のの掛け算の値を掛けた式を考えればよい。 　 12345 × … × 54321 / 100 = (12345 × 23456) / 10 × (98765 × 87654) / 10 × (残り６個の数の積) さらに (12345 × 23456) / 10 = (12345 / 5) × (23456 / 2) =　2469 × 11728 (98765 × 87654) / 10 = (98765 / 5) × (87654 / 2) = 19753 × 43827 となるため 　 12345 × … × 54321 / 100 = 2469 × 11728 × 19753 × 43827 × (残り６個の数の積) となる。この計算式の一の位は掛け算の数の一の位を掛ければよいため、 9 × 8 × 3 × 7 × 7 × 8 × 9 × 3 × 2 × 1 = 4572288 （赤の数字は 34567, 45678, 56789 の一の位、青の数字は76543, 65432, 54321 の一の位の積を表す）以上から 　 12345 × … × 54321 = （一の位が 8 の数）× 100 = 下三桁が 800 の数 　となるため、百の位は 8 である。

問題： 一辺が１の正方形ＡＢＣＤがある。辺ＡＤを直径とする円の中心をＯ、辺ＡＢ上の点Ｅを直線ＣＥが円Ｏの接線となるようにとる。このとき三角形ＣＢＥの面積を求めなさい。

問題：線分ＡＢと一本のひもがあります。ひもは線分ＡＢより短く、半分より長いですが長さは分かりません。 　このひもを使い、線分ＡＢの中点を求めなさい。

　今回もマスは一人で挑む。今回は数式を書いてしばし、すぐに解答を書いた。２週連続のマスの秒殺（この言葉も久しぶりだな）に焦る東大生。２人が確認をしてこちらも解答を出した。マスは余裕でお宮の作った袋リリアンで遊ぶ始末。

コマ大チーム ひもをグ〜〜っと伸ばしてＡＢの長さにして 半分に折る。 東大生チーム Ａ，Ｂから楕円を描いてその交点を線で結ぶ。 ＡＢとの交点が中点。 マス・ポヌペア ひもの端をＡに置いたときの反対の端をとり、 Ｂに対しても反対の端を取る。 　ひもで反対の端の間の長さの半分を取る。

正解…マスの方法は正解！！

ひもの端をＡに置く。このときの反対の端を固定したまま、Ａにある端をＢ に動かす。このとき、ひもの折れる部分が中点になる。

左の図の方法： 　ひもの端をＡに置き、ひもの半分の長さに印をつける。点Ｂから残りの長さを取り、 同じく半分の長さに印をつける。 　それぞれの半分の長さの２個の印の間隔がちょうどＡＢの半分の長さであるため、 ひもで長さを取り、ひもを移動させて中点を取る。 　右の図の方法も考えた。図から中点の取り方は分かると思うため省略。

問題：スニーカーとストップウォッチを使い√２を計りなさい。

　物理学に挑戦したかったマス。そして３週間ぶりの登場ポヌさん。２人の共同作業で計算を行う。するとスニーカーを落として時間を計測。さらにスニーカーをひもでぶら下げて揺らし始めた。何をしているのか、ということはおそらく見当がつくでしょう。

コマ大チーム	４人の１００ｍのタイムと足の大きさ。 それぞれの平均の比が√２になる。
東大生チーム	３９．２ｍのところからスニーカーを 落とす。 地面に落ちるまでの時間が√２秒。
マス・ポヌペア	振り子の１往復の時間が２．３４秒である ときのひもの長さが√２ｍになる。

正解…全員不正解！！だけどちょっと惜しい

問題：ピアノの白鍵のうち１オクターブ以内の２つの音を出して、１通りに聞き分けられる ２つの音はどれとどれでしょう。 　２つの音はたとえば「ファ」と「高いレ」などの可能性もある。

　好調が続くマス。しかし、今回はまったく答えが出ない様子。コマ大チームのところに置かれているキーボードでおもむろに曲を弾く。しかし答えは出て来ない。対して３連敗中の東大生。今回も苦戦を強いられている。中村先生からヒントとして「ドとレの間は半音が２個分、ミとファの間には半音が１個分ある」ということを聞く。そこでひらめいて一気に計算。笑顔で答えを書く。

コマ大チーム	すべての２音を 聞き分けられる	鍛えた絶対音感で挑戦。 結果は１勝１敗。
マス・ポヌペア	「？」の一文字	お手上げ、と一言。
東大生チーム	「ファ」と「シ」	この２音だけが「半音が６個分」 であることから。

正解…「ファ」と「シ」　東大生チーム正解！！

「ド」と「レ」の間には黒鍵がある。黒鍵はこの２つの音の中間にあたるため、「ド」と「レ」の間には「半音２個分」の差があると考えられる。同様にして「ファ」と「ソ」の間にも「半音２個分」の差があることがわかる。 　一方、「ミ」と「ファ」の間には黒鍵がない。これは「ミ」と「ファ」には「半音１個分」の差があることを表している。同様にして「シ」と「高いド」の間にも「半音１個分」の差がある。 つまり、２つの音の間に「半音が何個分あるか」を分かれば、２つの音の推測ができる。

実際に２つの音の間に「半音が何個分あるか」を調べて、表にまとめると以下の通りになる。 この表で上の行の「ミ」の下に書かれている「４」という数字は「ド」と「ミ」の間に半音４個分あることを表す。一方左の列の「ミ」の右に書かれている「８」は「ミ」と「高いド」の間に半音８個分あることを表す。 　この表の中で、赤で書かれた「６」を調べると「ファ」と「シ」の２音に対してのみ現れ、他の２音について「６」が現れていない。「６」以外の数字は表の中に２回以上現れている。 　このことから２つの音を聞いて、その２音の差が「半音６個分」であることがわかれば、「ファ」と「シ」の２音であることがわかる。

問題：１６本の木を植えて、木が４本並んだ列が１２列できるように並べなさい。

　冷蔵庫が小さいことが悩みの杉山さん。担担麺が好きだけど頼めない溝田さんと悩み多き（？）東大生。今回の問題は難問なのか、マスも東大生も悩みに悩んでいる。木を１２列並べられない。ここで竹内先生から一言「１２列より多い１３列以上の答えを出してもＯＫです」１３列以上できるのか否か、謎が謎を呼ぶ中時間が過ぎた。

　各組の解答は以下の通り。

コマ大チーム（左の図）…植木鉢を並べた写真を見せる。「１２列できた」と話したものの 調べたら点線部分が３個の植木鉢しかない。 マス・ポヌペア（中央の図）…色々並べたが答えは出せず。 東大生チーム（右の図）…図の並べ方では１０列しかできなかった。

緑の丸が木を表し、青の線で列を表す。