この2枚の紙の同じ位置のマス目に書かれたその数字をすべて 求めなさい。
「コマ大数学科」に挑む・13年6月
最終更新日2013年7月22日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 2013年問題(6/7) |
| 日常の数学(6/14) |
| はっぴぃえんど問題 (6/21) |
| 剛体の力学(6/28) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
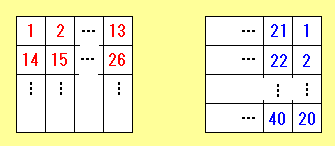
問題:たて20マス、横13マスのマス目が書かれた紙2枚それぞれに
1〜260の数字を図のように書いていく。 この2枚の紙の同じ位置のマス目に書かれたその数字をすべて 求めなさい。
|
満を持して登場の松本さん、一方ここしばらくの好調が止まってしまったマス北野。2組ともコマ大チームと同じように数字を書き並べていく。法則が見えてくるのか?そんな2組の後ろで数字を書いていくコマ大チーム。たたみ1畳近い紙に書いていく様子はさながら「文化祭の準備」みたいである。最後の最後で字のずれが発生したが、どうにか書き終えた。
| マス・ポヌペア | 87 | 同じ数字が現れそうな位置を 調べて出した。 |
| 東大生チーム | 87と174 | 1の位が「1」の場所を調べて から探した。 |
| コマ大チーム | 87と174 | 検証の結果 2枚の紙を重ねて答えを探した。 |
正解…87と174、東大生チーム、コマ大チーム正解!
この問題、答えの出し方は意外と簡単なのです。
|
左から x 番目、上から y 番目のマス目に書かれている数字をそれぞれの紙で求めていく。 1番目の紙では、一番上の列に書かれている数字はちょうど x である。また、一つ下のマス目に行くと数字が 13 増える。以上から、左から x 番目、上から y 番目のマス目に書かれている数字は x + 13 (y-1) = x + 13y - 13 と表すことができる。たとえば左から 3 番目、上から 3 番目のマス目の数字は3 + 13*3 - 13 = 29
240 + y - 20 (x-1) = -20 x + y + 260 と表すことができる。たとえば左から 3 番目、上から 3 番目のマス目の数字は-20*3 + 3 + 260 = 203 |
|
同じ位置に同じ数字が入るとき、上の2つの式が同じ値を取るため、
x + 13y - 13 = -20 x + y + 260
y = 7 ⇒ x = 9. この位置の数字は 9 + 13 × 7 - 13 = 87 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年6月
「日常の数学 (6/7)」
|
問題:堀のそこから生えている水草が水面から少しだけ見えています。
この水草を使い、堀の水深の求め方を考えなさい。
|
マスはこの問題を知っていたのか、すぐに図を描いて計算式を書いて、そして解答を書いた。一方東大生チームは図を描いて、そこで止まってしまった。道具を使った方法を考えてはいるが表情はいまひとつ。いわゆる「エレガント」な解答ではない様子。
| コマ大チーム | 潜水して、測る結果は5m |
| マス・ポヌペア | 「水草の水面より上の長さ」と「水草を斜めに して上端が水面に付くまでの距離」を使い計算する。 |
| 東大生チーム | 他の物の影の長さと水草の影の長さから計算する。 |
正解…マス・ポヌペアの方法が正解!!
この問題、私は知っていました。では解説です。
|
このとき、図から x, b, a+x の3辺の長さの直角三角形が出来上がる。三平方の定理から
(a+x)^2 = x^2 + b^2 ⇒ a^2 + 2 a x = b^2 |
|
例えば a = 1, b = 5 とすると x = (5^2 - 1^2) / 2*1 = 24 / 2 = 12 となる。実際、上の図の直角三角形は 5, 12, 13 の長さの直角三角形になる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年6月
「はっぴぃえんど問題 (6/21)」
問題:平面上に以下の条件でいくつかの点を置きます。
|
今回の東大生チームは杉山・溝田ペア。そしてスタジオに遊びに来た東大生チームOB山田さんも参加…その横に大神本舗も一応参加。新旧東大生、そしてマス・ポヌペアの対決はいかに?
| 東大生チーム | 6個 | 四角の頂点の中に2点という配置 |
| マス・ポヌペア | 8個 | 四角の頂点の中に4個ぐらい入れられるのでは という推測。 |
| コマ大チーム | 8個 | 検証の結果とは別の配置を考えていた。 四角の頂点の中に4個の点を入れた。 |
正解…8個、マス・ポヌペア、コマ大チーム正解!!
4個の点までは簡単に置くことができるが、5個目の点を置くときから注意が必要である。
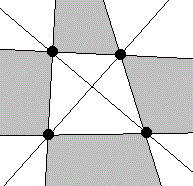 どの3点も一直線上にならないように4個の点を置く。このとき4点で四角形ができる。
このとき5個目の点を置ける場所を探す。
どの3点も一直線上にならないように4個の点を置く。このとき4点で四角形ができる。
このとき5個目の点を置ける場所を探す。
|
|
|
|
|
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年6月
「剛体の力学 (6/28)」
|
問題1:同じ大きさ、同じ重さのドミノをA.狭い間隔で並べたものと、
B.広い間隔で並べたもの。すべて倒れるのはどちらが早いでしょう。
|
| 東大生チーム | A.狭い |
| 明大チーム | A.狭い |
| コマ大チーム | A.狭い |
正解…A.狭い 全員正解!
今回は間隔を広げすぎたため遅くなった、ということ。普通の間隔と極端に狭い間隔のドミノでは普通の間隔(広いほう)が早くなるとのこと。今回は問題がたっぷり(?)ある。続いて第2問。
|
問題2:同じ大きさでA.軽いドミノを並べたものと、B.重いドミノを並べたもの。すべて倒れるのはどちらが早いでしょう。もちろんどちらも等間隔に並べる。
|
| 東大生チーム | B.重い |
| 明大チーム | B.重い |
| コマ大チーム | B.重い |
正解…B.重い 全員正解!
ドミノの速さはドミノのエネルギーによるが、エネルギーはドミノの重さに比例するため重いほうが早くなる、とのこと。続いて第3問。
|
問題3:大小さまざまなドミノをA.小さい順に並べてもの、とB.大きい順に並べたもの。すべて倒れるのはどちらが早いでしょう。ただし並べた長さはどちらも同じである。
|
| 東大生チーム | B.大きい順に並べたもの |
| 明大チーム | B.大きい順に並べたもの |
| コマ大チーム | B.大きい順に並べたもの |
正解…B.大きい順に並べたもの 全員正解!
やはり大きいものが小さいものを倒す力は、小さいものが大きいものを倒す力に勝っているため、ドミノも進みやすいのである。では、大小の順番を組み合わせたらどうなるのか?これが最後の問題。
|
問題3:大小さまざまなドミノをA.山型(前半は小さい順、後半は大きい順)とB.谷型(前半は大きい順、後半は小さい順)。すべて倒れるのはどちらが早いでしょう。ただし並べた長さはどちらも同じである。
|
| 東大生チーム | A.B.同時の早さ | 一言「直感」 |
| 明大チーム | B.谷型 | 前半の速さを維持したまま 倒れるのでは、と推測 |
| コマ大チーム | A.山型 |
正解…A.山型 コマ大チーム正解!
実は、この問題に関してはどちらが早いのかは解明されていない、とのこと。ただ、実際に試して山型が早いから「山型が早い」という結論に達した。今回は「コマ大フィールズ賞」ではなく「コマ大ノーベル賞」。受け取ったのは最後の問題を見事当てて(?)しかもドミノを並べた、ということでコマ大チーム。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年6月