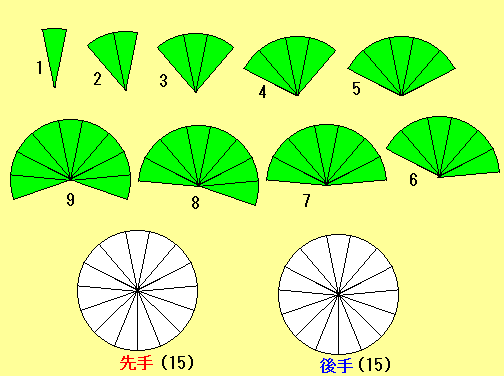
図のような9個のピースを2人が交互に円の上に並べていき、3枚目で円を完成させたら勝ち、というゲームをする。
このゲームを有利に進める作戦を求めなさい。
「コマ大数学科」に挑む・13年8月
最終更新日2013年9月29日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 必勝法 Part 10 (7/19) |
| 配置ーズ (8/9) |
| 力学(8/16) |
| ハミルトン閉路(8/23) |
| 辞書学(8/30) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「必勝法 Part 10 (8/2)」
|
問題: 図のような9個のピースを2人が交互に円の上に並べていき、3枚目で円を完成させたら勝ち、というゲームをする。 このゲームを有利に進める作戦を求めなさい。
|
コマ大が始まってからずーっと定位置(低位置?)でおなじみのコマ大チーム。今回は「丸い」食べ物をゲットするために「丸」の内にやってきた。丸い食べ物としてピザやケーキが登場。しかし、食べるためには問題のゲームに勝たなければならない。必死に作戦を練るが努力は実らず2連敗。最後に吉田プロデューサと対決して勝ったものの、いただけた食べ物は夏みかん1個。で、必勝法は見つかったの?
必勝法といえばマス北野。マス北野といえば必勝法(?)というほど「必勝法」シリーズに強いマス北野。今回もひらめいた模様。円を使った問題なのに、紙にマス目を書き始めた。木村さんとしばし話したあと竹内先生のところへ向かう。実際にゲームをして自分の考えに確信を持った。一方東大生チームも実際にゲームをしながら解答を導き出す。東大生はマスの閃きに勝つのか?
| コマ大チーム | 先手が「5」を選ぶ | 検証の結果 |
| 明大チーム | 先手が「5」を選ぶ | 魔方陣を作り、1列を作るように 数字を選んでいく。 |
| 東大生チーム | 後手で「5」を選ぶ | 後手になって「5」を選べば うまくいく…みたい。 |
正解…明大チームの解答が正解!
マスのひらめきが見事に的中。では詳しい解説です。
|
問題の9個のピースで円を作ることができる組み合わせは以下の8通り。
「9,5,1」「9,4,2」「8,6,1」「8,5,2」 これらはすべて3×3の魔方陣の1列の数字に入ることができる。
|
|
そこで先手がこの魔方陣の中央にある「5」を選べば、まず引き分けに持ち込むことができ、
負けることはない。
そのあと、先手は1列を作る残り1個の数字を選んで勝ちになる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年8月
「配置ーズ (8/9)」
|
問題: 男性3人、女性3人の計6人で写真を撮る。6人は背の高さの順番が男性と女性が交互になっている。 6人が横1列で写真を撮ったとき、それぞれの女性の左に必ずその女性より背の高い男性がいる確率を求めなさい(女性と女性より背の高い男性の間は離れていてもよい)
|
確率といえばマス…の苦手分野。しかし、木村さんがフォローをしていく。一方の東大生チームは場合分けをしてしっかりと条件に合う並びを数えていく。いち早く答えを書いたのはマス北野。しかし、答えを書き直して計算を確認している間に東大生も解答。
| コマ大チーム | 4/26 | 27枚の写真のうち1枚が失敗。 残りの26枚中4枚が条件を満たす。 |
| 明大チーム | 5/16 | 女性が並ぶことができる場所を調べた。 |
| 東大生チーム | 7/24 | 一番背の高い女性の位置で 場合分けをして調べた。 |
正解…5/16 明大チーム正解!!
見事正解の明大チーム。説明についても中村先生が「そのまま」と一言。ではその説明を。
|
6人を背の高い順から「男1、女1、男2、女2、男3、女3」と表すことにする。 男1と女1の並び方は2通りあるが、条件を満たす並び方は「男1女1」の1通りしかない。つまり確率1/2で条件を満たす。 |
|
次に先ほどの2人に男2がどこに入るかを考えると「左端」「2人の間」「右端」の3通りある。しかしいずれも問題の条件を崩すことはない。つまり 男2男1女1 男1男2女1 男1女1男2 のいずれの並び方でも条件を満たす。
このあと女2がどの位置に並ぶことができるかを考える。今回は「左端」「左から2番目」「右から2番目」「右端」の4通りの位置がある。しかし上の3通りのいずれの場合も女2は「左端」以外であればどの位置に並んでも条件を満たす。 男1女2男2女1 男1男2女2女1 男1男2女1女2 のいずれの並び方でも条件を満たす。つまり、男2、女2の並び方は確率3/4で条件を満たす。 |
|
同様の考え方で、男3、女3が加わる並び方を考える。 男3が並ぶ位置は5通りあるが、いずれでも条件を満たす。 女3が並ぶ位置は6通りあるが、左端以外であればどの位置で並んでも条件を満たす。 つまり、男3、女3の並び方は確率5/6で条件を満たす。 以上から、問題の条件を満たす並び方になる確率は1/2×3/4×5/6=5/16となる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年8月
「力学 (8/16)」
|
問題:A,B2チームが綱引きを行う。Aは背の高い順に並び、Bは背の低い順に並ぶ。この状態で綱引きをした時、どちらが勝つでしょう。ただし、2チームの体重の合計は同じものとする。
|
| 明大チーム | A:背の高い順 | 引く力が下にかかるため |
| 東大生チーム | B:背の低い順 | 力のモーメントを考えた結果 |
| コマ大チーム | A:背の高い順 | 検証の結果 |
正解…A:背の高い順
背の高い順に並ぶと引っ張る力が下向きになる。逆に背の低い順では引っ張る力が上向きになる。下向きの力がかかりやすいため、背の高い順が有利になる。続いてこんな対決。
|
問題:A,B2チームが綱引きを行う。Aは綱の前の位置に並び、Bは綱の後ろの位置に並ぶ。この状態で綱引きをした時、どちらが勝つでしょう。ただし、2チームの体重の合計は同じものとする。
|
| 明大チーム | B:綱の後ろの位置 | 2チームの中心がBに近いため |
| 東大生チーム | B:綱の後ろの位置 | 力のモーメントを考えた結果 |
| コマ大チーム | A:綱の前の位置 | 検証の結果 |
正解…力学的には同じ(引き分け)
力の向きが平行で、力の大きさが同じであれば釣り合うため、とのこと。しかし検証では心理的にAチームの力が強かったのでは?とのこと。検証を見た感じではBチームが左右に振られて力が入れにくかったのでは、と思った。それはさておき、綱引き対決はまだ続きます。
|
問題:A,B2チームが綱引きを行う。Aは綱の中央に集まり、Bは均等に分かれて並ぶ。この状態で綱引きをした時、どちらが勝つでしょう。ただし、2チームの体重の合計は同じものとする。
|
| 明大チーム | B:均等に分かれて | 摩擦が分散されるため |
| 東大生チーム | 引き分け | 力が同じになるため |
| コマ大チーム | B:均等に分かれて | 検証の結果 |
正解…B:均等に分かれて並ぶ
中央に集まると後ろに倒れにくくなるため、力が弱まる、とのこと。確かに検証ではAチームはやりにくそうだった。4問目はこんな対決。
|
問題:A,B2チームが綱引きを行う。Aは綱の片側に立ち、Bは綱の両側に立つ。この状態で綱引きをした時、どちらが勝つでしょう。ただし、2チームの体重の合計は同じものとする。
|
| 明大チーム | B:両側に立つ | 長期戦になると強いかも? |
| 東大生チーム | A:片側に立つ | 力の方向が分散しないため |
| コマ大チーム | B:両側に立つ | 検証の結果 |
正解…B:綱の両側に立つ
綱の片側に立つと、その方向に力がかかりやすくなり、相手を引っ張る力が弱くなる。一方両側に立つと、綱の上に力が集まり、相手を引っ張る力が強くなる。さて、ここまでの4回の対戦で2対2と拮抗している検証の2チーム。最後の対戦として、各チームがこれまで行った配置で最強と思われる配置で挑んだ。その対決はこちら。
|
問題:A,B2チームが綱引きを行う。Aは綱の前に集まり、Bは綱の両側、しかも均等に並ぶ。この状態で綱引きをした時、どちらが勝つでしょう。ただし、2チームの体重の合計は同じものとする。
|
| 明大チーム | B:両側、均等にならぶ | バランスが良いため |
| 東大生チーム | B:両側、均等にならぶ | Aの態勢のときは 偶然勝ったため |
| コマ大チーム | A:中央に集まる | 検証の結果 |
正解…B:両側、均等に立つ
理論上はBが強い。しかし、検証は「根性の勝利では?」と竹内先生。前回のデートをすっかり忘れて検証も終了。この5問で明大チームは4問、東大生チームは1問。コマ大チームは3問。というわけでコマ大「ノーベル賞」は圧倒的な強さの明大チーム。ちなみに私は2問でした。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年8月
「ハミルトン閉路 (8/23)」
|
問題: 隣り合う2個の数字の和が常に平方数になるように、1から15の数字を並べなさい。
|
問題開始、と共に一気に答えを出したのは明大チームの木村さん。何やら作戦を考えていた模様。東大生チームも遅れるものの、しっかりと正解を導いた。
| コマ大チーム | 9,7,2,14,11,5,4,12,13,3,6,10,15,1,8 | 検証の結果 |
| 明大チーム | 和が平方数になる数字同士を 線で結んで考えた | |
| 東大生チーム | 和が平方数になる数字の 組み合わせを考えた |
正解 … 9,7,2,14,11,5,4,12,13,3,6,10,15,1,8 全員正解!
東大生チームは和が平方数になる数字の組み合わせを書き並べて考えたが、明大チーム木村さんが一気に答えを出す方法を使っていた。
|
2つの数字の和で最小は 1+2 = 3, 最大は 14+15 = 29 であるため、和になる可能性のある平方数は 4, 9, 16, 25 の4個。それぞれの平方数について、和がその平方数になる2つの数を調べると以下の通りになる。
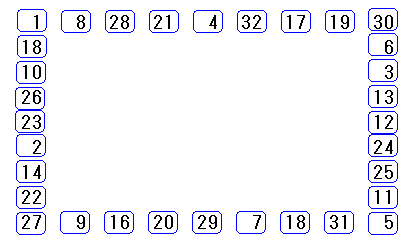
4 : 1+3 これらの和が平方数になる2つの数を線で結ぶ図を作ると以下の通りになる。
この図で、8 と 9 は1本ずつしか線が出ていないため、問題の条件にあうように並べるときこの2個の数字が両端になる。9 から線に沿って進んでいくと、 9,7,2,14,11,5,4,12,13,3 と並べていくことができる。3 の次は 1 と 6 に分かれている。1 に進むと 1, 8 となり、すべての数字を使わずに 8 に行く。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年8月
「辞書学 (8/30)」
国語辞典には様々な言葉の意味が書かれている。しかし目に見えないものに対しての意味の解釈は辞書を作っている出版社によって特色が出てくる。たとえば「右」という言葉の意味も「東を向いたとき南にあたる方角」「アナログ時計の文字盤の1時から5時のある方向」など様々。そこで、コマ大メンバーにも言葉の意味を作ってもらう。
| 問題:「恋愛」という言葉の解釈を書きなさい。 |
| 東大生チーム
愛しいと感じるときもあれば、時に |
明大チーム
精神と空間を共有したいという |
コマ大チーム
初めてのときめきが永遠に続く |
| 初版
一組の男女が交互に相手にひかれ、ほかの |
第五版
特定の異性に特別な愛情をいだき、高揚した |
| 恋愛:男女間の恋い慕う情(岩波国語辞典より) |
では、特色のある辞書で問題を作ってみよう、ということで出されたお題はこちら。
| お題:ある言葉の解釈に使われる言葉をさらに解釈の文章に変えてみる。 |
|
例題:次の文章は何を表しているのか?
動物の頭・胴・手足などのすべてをまとめたものに |
|
「動物の頭・胴・手足などのすべてをまとめたもの」⇒「体」 「その全体または上半身にまといつけるもの」⇒「着る」 「酸素と水素の化合物」⇒「水」 「清潔さ、純粋さなどを失うことを取り去る」⇒「洗う」 「電流が単位時間にする〜行為をするもの」⇒「機械」 ということから問題の文章は 体に着たものを水などで洗う機械 となり、これは「洗濯機」を表している。 |
|
コマ大チームからの出題
一定の期間、学問、経験、年齢、地位などが |
東大生チームからの出題
炭素、水素から成る糖とアルコールの一種である物を |
明大チームからの出題
温度や気圧の差でおこる空気の |
|
コマ大チームからの出題
「一定の期間〜自分より上の人」⇒「先輩」
ということから問題の文章は「ねずみ花火」 |
東大生チームからの出題
「炭素、水素〜固めた状態のもの」⇒「寒天」 となることから問題の文章は
寒天を熱を通して柔らかくどろどろと ということでこの文章は「水ようかん」を表している。 |
明大チームからの出題
「温度や気圧の〜空気の流れ」⇒「風」 となることから問題の文章は
風によって中に下がっている舌 となり、これは「風鈴」を表している。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年8月