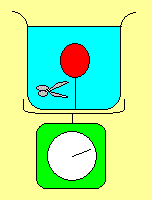
この容器を秤に載せて、ひもを切った直後、秤の表示はどうなるでしょうか?
「コマ大数学科」に挑む・13年9月
最終更新日2013年10月17日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 夏休み実験SP (9/6) |
| サイクロイド (9/13) |
| 視聴者からの挑戦状 Part 9(9/20) |
| アブー・アルワファー(9/27) |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「夏休み実験SP (9/6)」
|
問題:空気を入れた風船が、ひもで容器の底に結び付けられて水に
使っています。 この容器を秤に載せて、ひもを切った直後、秤の表示はどうなるでしょうか?
|
| 明大チーム | 表示は変わらない | アルキメデスの原理より |
| 東大生チーム | 軽くなる | ひもの張力が無くなるため |
実際に問題の通りに容器の底にひもでつながれた風船を付け、水を入れる。このひもを切ろうとするが、水があふれたり秤の表示が動いたりしてうまくいかない。そこで登場したのは春雨。ひもの途中を春雨でつなぎ、溶けて切れるまでじっくり待つ。そして出た解答は…
| コマ大チーム | 軽くなる | 実験の結果 |
正解…軽くなる コマ大チーム、東大生チーム正解!!
私は「変わらない」と思っていた。
|
風船がひもで容器の底でつながっているとき、風船が引っ張る力(張力)が上向きに
かかっている。張力に釣り合うため、容器は下向きに同じ力がかかっている。この力
は秤にもかかっている。 ひもが切れたとき、風船の張力が無くなる。それに伴って、容器にかかっていた 下向きの力もなくなる。秤からもこの力がなくなるため、秤の針は一瞬軽くなる方向に 動く。
|
|
問題:ニンジンが図のようにひもで水平に吊るされています。ニンジンをひもの位置で2つに切り、それぞれの重さを比べたとき、次のどれが成り立つでしょうか?
ア.A(へたのある方)が重い
|
| 明大チーム | ウ.同じ重さ | 「ひっかけかも」と一言 |
| 東大生チーム | ア.Aが重い | (説明はなし) |
| コマ大チーム | ウ.同じ重さ | 釣り合うから同じ重さ? |
正解…ア.Aが重い 東大生チーム正解!!
解説は以下の通り。
|
ニンジンが図のように釣り合っているとき、Aのニンジンの端はひもから近い距離の所にあり、
Bのニンジンの端はひもから遠い距離のところにある。一般に釣り合っているとき
(ひもまでの距離)×(かかる重さ) は両端とも一定の値を取る。このためひもから近いほど、重さは重くなる。このため AのニンジンがBより重い。
|
|
問題:滑車に掛けられた綱の一方の端にはおもりが吊るされており、もう一方の端にはおもりと同じ重さのサルがいます。 この状態でサルが綱をよじ登った場合、サルやおもりの位置はどうなるでしょうか?
|
今回の「コマ大ノーベル賞」は2問を正解した東大生チーム。実に2か月ぶりの東大生チームの勝利であった。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年9月
「サイクロイド (9/13)」
|
問題:直角に折れ曲がった線の内側を端から端まで
円を転がします。 スタート時に線に触れていた円周上の点をPとすると、点Pが初めて線に触れたのは円を端まで転がし終わった時でした。 この円の半径を求めなさい。 ただし円周率は3として考える。
|
今回の2組は静かに計算を始めた。着々と計算を続けた答えを出した2組。しかし、この計算は意外な展開の序章に過ぎなかった?
| コマ大チーム | 20.65cm | 検証(計算)の結果 |
| 明大チーム | 20cm | 円の転がる様子を図に書いて計算 |
| 東大生チーム | 20cm | 円の転がる様子を図に書いて計算 |
正解…20cm と 10.4cm 明大チーム、東大生チーム一つだけ正解!
答えが2つあることを知り「あっ」と気づく東大生。私はこの問題は知っていました。ということで解説。
|
円をスタートの地点から直角の部分まで回転させる動きと、
ゴールの地点から直角の部分まで逆回転させる動きを見ると、
ちょうど直角の2等分線に対して対称の動きをする。 このため、直角で円が方向を変えるとき、点Pはその2等分線 (青線)の上にあることがわかる。
|
|
|
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年9月
「視聴者からの挑戦状 Part 9 (9/20)」
|
問題:
ABCD は AB = 3 cm, BC = 4 cm の長方形。
点 P, Q は AP = DQ = 1 cm を満たし、
AR は中心が Q 半径が AQ の円の一部、
DR は中心が P 半径が DP の円の一部である。
この図形に内接する正方形を図のように描いたとき
この正方形の一辺の長さを求めなさい。
|
長い間肩透かしを食らいながら、やっとで連絡がついたのは東大生OB「秒殺シスターズ」の衛藤さん。快く引き受けてくれた衛藤さんに問題を送って後は返事が来るのを待つだけ。ということでラジオ番組は終了となった。
いつものように計算を始める東大生チーム。答えが出た模様。一方の明大チームは作図をして考えようとするが、図が大きすぎて手間取ってしまう。答えは出たのでしょうか?
ちなみに、今回の問題を送られた方は元俳優で現在は高校の数学教師をされている方。入試用に作った問題で、中学生でも解ける、とのこと。
| コマ大チーム | 18/5cm | 衛藤さんの解答。 |
| 東大生チーム | 18/5cm | 座標を使って計算 |
| 明大チーム | 3.6cm | 神様が舞い降りて解答?? |
正解…18/5(=3.6)cm 全員正解!!
マスは図を描いて長さを測る方法を取ったみたいである。東大生とコマ大を助けた衛藤さん(ついでに私)はいずれも座標を使って答えを求めた。
|
|
|
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年9月
「アブー・アルワファー (9/27)」
|
問題:一辺aの正方形が3つある。これらを切って組み合わせて、一つの正方形を作りなさい。 ただし、切った物はすべて使い、重ねることもできない。
|
残り2回といえども、黙々と問題を解いていく2組。前回「神が降りてきた」と話したマスも、「神」ではなく「紙」を切って並べていく。風車のような形に並べたところで何か閃いて、正方形を作り上げていく模様。東大生チームはまずは計算。そのあと紙を切り始めた。明大チームから少し遅れて正方形を作ることができた。
コマ大チームの解答はちょっとしたモザイクアートのためここで見せることはできない。明大チームと 東大生チームの解答は以下のとおりである。
|
明大チームの解答
|
東大生チームの解答
|
正解…明大チームの解答が正解!!
コマ大チームは中村先生からの指摘を受けたところ、ジャージから使われていない紙の破片が見つかった。つまり、全部使われていなかった。残念??
|
私の解答
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年9月