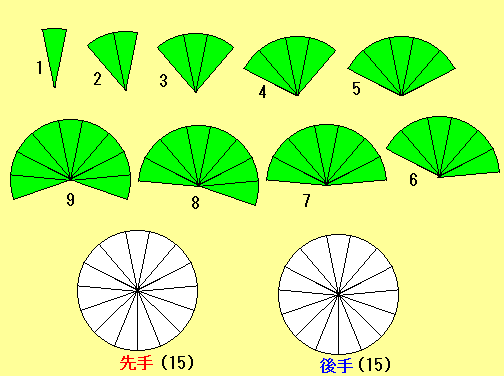
図のような9個のピースを2人が交互に円の上に並べていき、3枚目で円を完成させたら勝ち、というゲームをする。
このゲームを有利に進める作戦を求めなさい。
「コマ大数学科」に挑む・13年10月
最終更新日2013年11月13日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| コマ大最終回だよ 全員卒業! 前半 (10/5) |
| コマ大最終回だよ 全員卒業! 後半 (10/5) |
| コマ大プレイバック 必勝法 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
問題:次の数列の□に入る数字は何でしょう。
0,2,3,2,5,5,□,10,12 |
正解…7 全員正解!
この数列は4番目以降に法則がある。その法則は至ってシンプル、「2つ前の数と3つ前の数を足した数」を並べていくだけ。
|
4番目の数:2番目の数+1番目の数=2+0=2 5番目の数:3番目の数+2番目の数=3+2=5 6番目の数:4番目の数+3番目の数=2+3=5 7番目の数:5番目の数+4番目の数=2+5=7 8番目の数:6番目の数+5番目の数=5+5=10 漸化式で表すと x_{n+3} = x_n + x_{n+1} |
|
問題の数列は p が素数のとき、p 番目の数は必ず p で割り切れる という性質を持つ。実際、上の数列の2,3,5,7番目の数はそれぞれ2,3,5,7 である。この後も数列を続けて作っていき、50番目まで調べていくと
11番目= 22=11× 2 と素数番目は必ずその素数で割り切れる。 |
|
問題:次の式の□に入る整数は何でしょう。
91=□^3+□^3=□^3+□^3 ただし、□に入る数字は負の数でもOK |
| 明大チーム | 91=3^3+4^3=(−5)^3+6^3 |
| 東大生チーム | 91=3^3+4^3=(−5)^3+6^3 |
| コマ大チーム | 91=3^3+4^3=4^3+3^3 |
正解…91=3^3+4^3=(−5)^3+6^3 明大チーム、東大生チーム正解!
この問題は地道に計算していくしか方法はない模様です。私も一応正解は出しましたが、最初は平方数をずっと調べていた。最後の最後でこんな凡ミスはしたくなかった。
|
整数の3乗の和で表すことができる正の数の中で、2通りの和で表すことができるものは問題の91が最小である。 条件を狭めて、正の整数の3乗の和で表すことができる正の数の中で、2通りの和で表すことができるものを調べると 1729=1^3+12^3=9^3+10^3 が最小である。この1729という数はラマヌジャンがタクシーのナンバープレートの数がこの性質を持つ、と指摘したことからの「タクシー数」と呼ばれている。 |
以上でコマ大のすべての問題が終わりました。後半はコマ大7年間の歴史を振り返っていきます。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年10月
「コマ大最終回だよ 全員卒業! 後半 (10/5)」
| 第10位 | ミスコマ大は音声さん |
2007年に放送された「コマ大学園祭」で男性陣によるミスコマ大を決めた。 1位に選ばれたのはスタッフの音声さん。かつてミス立教だった戸部アナは3位以内にも入れず。 |
| 第9位 | 全員で数独大会 |
2007年に放送された「オイラー」はスイス大使館で行われた数独大会の模様を伝えた。 その大会の決勝問題を出演者・スタッフ全員で挑戦。机に向かって問題を解く出演者、カメラで写しながら、スタッフルームで画面を切り替えながら数独の問題を解くスタッフも放送された。 |
| 第8位 | 戸部アナ結婚 | 番組内で「私の未来の旦那様」などとコメントをしていた戸部アナ。2012年にめでたく入籍を発表。それ以降はお惚気たっぷりのコメントを連発。 |
| 第7位 | ハプニング続出 |
150回記念のオープニングコメントで薬玉が割れない戸部アナ。懐かしの遊び「釘指し」でとんでもない所に釘を投げ飛ばす戸部アナ。 そして、会心のマジックを大失敗した東京大学奇術愛好会などなど、数え上げたらきりがないかも。 |
| 第6位 | コマ大フィールズ賞の 行方は… |
東大生チームOGの松江さんがスタジオを見学。傍らには旦那さんが一緒。2人そろってコマ大の問題を解いたところ松江さんだけが正解! 悩みに悩んだコマ大フィールズ賞は正解を出したので松江さん夫妻に渡る結果に。 |
| 第5位 | マス北野に助っ人登場 |
番組当初から一人で問題に挑み続けたマス北野。そんなマスに配慮してか、2007年にマスの助っ人が参加。 助っ人はベナン共和国からやってきた東大生のポヌさん。コマ大の問題を解いてきたポヌさんだったが、日本語は片言なので苦労することもしばしば。それ以外にも笑って踊って絵も描いて、とひょうきんぶりも披露した。 |
| 第4位 | 番組最高視聴率は? |
7年半にわたり放送されたコマ大の中で最高視聴率を取ったのは、コマ大チームの検証で林家ぺー・パー子さんが登場したときの5.0%。 数学 ⇒ 数字 ⇒ 誕生日 というつながりなのか、ぺー・パー子さんはコマ大にたびたび登場し、相変わらずのハイテンションを見せていた。 |
コマ大重大ニュースもベスト3が残された。はたして1位はどんな事件(?)なのか。
| 第3位 | 個性豊かな出演者 |
コマ大の花だった東大生チーム。最初は2人だったが、突然6人、そして5人の大所帯となった。かわいい系あり、切れ者系あり、天然系ありと個性も豊か。 さらにコマ大チームの検証にもたびたび登場したDrコバさんなど、ときどきレギュラー陣を超える活躍?を見せることもあった。 |
| 第2位 | エミー賞にノミネート |
深夜の番組でありながら、世界のテレビ界で最高の賞であるエミー賞の最終ノミネートに選ばれた。 惜しくも賞を取ることはなかったが、テレビ界に大きな功績を遺したことは確かかもしれない。それにしても大泣きした関ディレクターにはレギュラー陣も驚いた。 |
| 第1位 | マス北野皆勤賞 |
この番組の発案者でありながら、自ら問題を解く側に立ったマス北野。休むことなく出演を続けたのは当たり前といえば当たり前だが、何かと問題を起こすマスを考えるとすごいことである。 悩み、笑い、苦しむ、歌う、暴れる…あくまで数学と笑いにこだわったマスに感服です。 |
最後は7年半を通じての「グランドコマ大フィールズ賞」の授与です。これまでの3組のコマ大フィールズ賞の受賞数を調べたところ
|
マス北野 :130回 東大生チーム:154回 コマ大チーム: 37回 |
-----------------------------------------------------------------------------------------------
かくして「たけしのコマ大数学科」が終了しました。おそらく私を含め番組が終わることを残念に思う方々もいるはずです。私も残念ながら、書き続けた「コマ大数学科に挑む」を終了することに…と思ったのですが
今年はあと2か月半ほどありますので、今年いっぱいはコマ大の問題についてあれこれ書いていく「コマ大プレイバック」を載せていきたいと思います。お暇がありましたらご覧ください。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年10月
「コマ大プレイバック 必勝法」
|
問題: 図のような9個のピースを2人が交互に円の上に並べていき、3枚目で円を完成させたら勝ち、というゲームをする。 このゲームを有利に進める作戦を求めなさい。
|
この問題に関しまして「先手が1を選んでも負けることはないのではないか」というメールをいただきました。この質問を検証してみました。
|
先手が1を選んだあと、後手が選ぶ数字によって場合分けをすると…
後手が5以下を選んだ時は、次に先手が8を選べば引き分けになる。
|
これまでの必勝法問題をまとめてみます。カッコ内は放送回のテーマです。
|
第1回(必勝法): 3個、5個、7個の3つの石の山のうち、一つの山から石を取っていく。2人が交互に取り最後に石を取り終えた方が勝ち。 このゲームの必勝法は? |
第2回(ゲーム理論): 2人がじゃんけんをして、グーで勝つと3段、チョキ、パーで勝つと6段階段を上がっていく。 このとき、グー、チョキ、パーをどのように出して行けば有利か? |
|
第3回(スイッチングゲーム): いくつかの点と、それらの点をむすぶいくつかの線がある。 先手は決められた2点をむすぶ線をつないでいく。後手は線をつながれないように線を切っていく。 先手が勝つための最低手数は何手か? |
第4回(橋ゲーム): 先手は上下に橋を一続きになるように橋を作っていく。後手は左右に橋を一続きになるように橋を作っていく。 先に一続きの橋を作った方が勝ち。このゲームの必勝法は? |
|
第5回(31): トランプの1〜6のカード24枚を2人が交互に1枚ずつ取る。2人が取ったカードの合計を31にしたら勝ち。先手はどのカードを取れば勝てるか? |
第6回(サイコロ必勝法): サイコロを2人が交互に転がす。ただし、裏返して反対の面を出すことはできない。上の面の目の数の合計が13になったら勝ち。このゲームの必勝法は? |
|
第7回(必勝法 Part 7): 1〜100まで書かれた盤面で、先手は1からスタートし、+1, +2, +10, +20 した数に進むことができる。 後手は100からスタートし -1, -2, -10, -20 した数に進むことができる。 先手の数が後手の数より超えるように動かざるをえなくなった時に勝敗が決まる。このゲームの必勝法は? |
第8回(必勝法 Part 8): 1〜10の整数を二人が交互に選んでいく。ただし、既に選ばれた数字の約数を選ぶことはできない。 数字を選ぶことができなくなったら負け。このゲームの必勝法は? |
|
第9回(テラガ・ブルク): 先手と後手は2個ずつのコマを持っている。盤面上にそれらのコマを置き、交互に自分のコマを1個動かしていく。相手を動けなくさせたら勝ち。 このゲームの必勝法は? |
第10回(必勝法 Part 10): 9個のピースを2人が交互に円の上に並べていき、3枚目で円を完成させたら勝ち、というゲームをする。 このゲームを有利に進める作戦を求めなさい。 |
一応、分類をしましたが、第10回が他と異質な一点あります。それは「ゲームの勝敗を決める手数が決められている」ということです。他のゲームは何手で終わるかははっきりわかりません。しかし第10回のゲームは「3枚目で円を完成させたら勝ち」と手数の指定が決められており、2枚目で円を完成させることは認められていません。
手数が決められた理由を考えると、おそらく「魔法陣」を使わせるためではないか、と思われます。魔方陣を使うとこのようにゲームを進めることができます、という説明をするために「3枚目で円を完成させたら勝ち」という制限を付けたのではと考えられます。
今年4月、コンピュータの将棋対局ソフト5台と将棋の棋士5人の対戦が行われ、コンピュータの勝利するというニュースがありました。これらの将棋ソフトは上の分類でいえば「しらみつぶし」型に近い内容だと思われます。コマ大で出された必勝法の問題はこれらの将棋ソフトを生みだず基礎であると言ってもおかしくありません。近い将来「じゃんけんに勝つソフト」が生まれるかもしれません。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・13年10月