数学とクイズでくつろいで<数学の部屋<「算数」と「数学」の間で<「算数」と「数学」の間で その4
「算数」と「数学」の間で その4
最終更新日2007年12月29日
人々の頭を悩ませ続けている算数と数学についてあれこれそれどれ書いています。一応難しい話は抜きで…というつもりで書いています。お茶もお菓子もありませんがごゆっくりお過ごしください。ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
ここでは
「紙を折って竜を作る?」「紙を折って竜を作る?…の続き」「紙を折って竜を作る?…その後は?」を加えました。
紙を折って竜を作る?
今回はまず写真を使って話を進めていきます。

まず細長い紙を用意します。上の写真のように赤線に沿って半分に折ります。もう一回折ってみます。矢印のように「右方向に折る」…このことに注意してください。青線は前の折り目のところです。

あと2回同じように半分に「右方向に折り」ます。最後の1回は折りにくいですが頑張って。さてこの紙を広げて、できた折れ目を直角にすると…

写真では分かりにくいので図で書くと右のようになります。
これからが問題です。先ほど右方向に4回折りましたが、これを右、左、右、左と左右交互に折り紙を広げると、どのような形ができるでしょう。

(こんな折り方。2回目が逆方向の降り方)
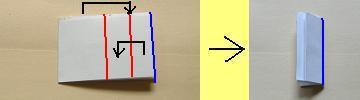
(こちらも同じく2回目が逆方向の降り方)
頭を使って考えるよりも手を使うのが手っ取り早いです。そこら辺の新聞でもチラシでも使って折ってみてください。答えと解説は次回。
紙を折って竜を作る?…の続き
前回の問題…


上の写真のように細長い紙を右、左、右、左と交互に半分に折って、紙を広げるとどのような形になるか、答えは次のようになります。

前回の右方向に折り続けた時の形とは全く違うものになりました。
では、同じように細長い紙を「右、右、右…」と「右、左、右…」とそれぞれ10回折って紙を広げるとどのような形になるでしょう?早速長さ2メートルほどの紙を用意して…と、わざわざ準備しなくて構いません。パソコンを使ってチョコチョコと計算するとそれぞれどんな形になるかすぐにできます。
すごいでしょ〜〜
と自慢しても仕方ないのでどんな形になるかお見せします。まず、「右、右、右…」と同じ方向に10回折り紙を広げるとこのような形になります。

紙を折って広げた形ですので実際は一本の線(折れ線)で書かなければいけませんが簡略化しました。このように同じ方向に何回も紙を折って広げてできる一本の曲線のことを一般に「Dragon Curve(竜の曲線)」と呼んでいます。竜の姿をしている…といえばしているような感じですが、個人的には
ラーメンの丼の縁の模様に見えます。
さて、一方の「右、左、右…」と交互に折った場合はどうなるか。ご覧ください。
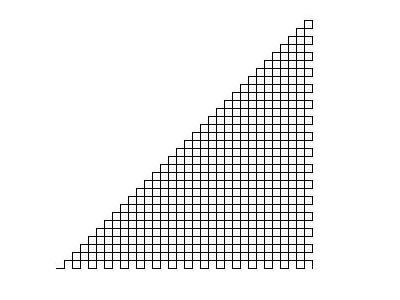
ほぼ三角形になっています。この後も右、左…と交互に折っていくとドンドン三角形に近くなります。また、右、左の順番を適当にして様々な折り方をすると様々な形を作ることができます。
さて、前回のものも含めてこれらの形にはある特徴があります。それは何でしょう。答えは次回。ヒントは「同じものをたくさん使います」
紙を折って竜を作る…その後は?
これまで2回に渡って紹介した「Dragon curve」と呼ばれる折れ線、これらにはどのような性質があるのでしょうか?
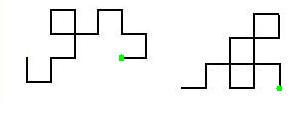
左の形を例に挙げて話していきます。緑の印がついた端を中心にこの折れ線を90度ずつ回転させて行きます。
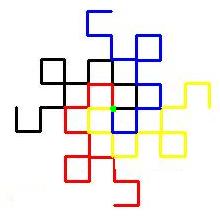
さらにこの形を並べていきます。
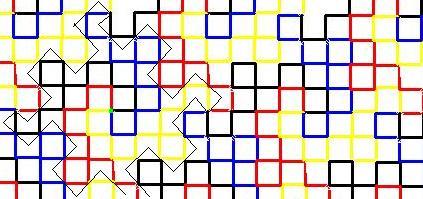
細い線で囲まれて部分が前の形です。このように並べ続けても他の部分と重なることも空白ができることもなく格子の形を作ることができます。
もう一つの折れ線も緑の印がついた端を中心にを90度ずつ回転させて、それを並べていくと…
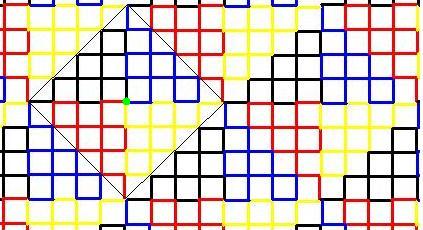
こちらも同じように他の部分と重なることも空白ができることもなく格子の形を作ることができます。この場合は線で囲まれた部分はちょうど正方形になっています。よく分からない折れ線でしたが4つ集めるときれいに正方形ができます。
このような性質は上の2つだけでなく、前回見せました10回紙を折ったときにできる折れ線でも同じことができます。ただ複雑に線が引かれているみたいですが、こんな性質があるのです。ぜひ皆さんも様々な Dragon curve
を作ってみてください…
えっ?めんどくさい…
そんな皆さんのために簡単に Dragon curve を作ることができるJAVAアプレットを次週ご紹介します。
数学とクイズでくつろいで<数学の部屋<「算数」と「数学」の間で<「算数」と「数学」の間で その4