数学とクイズでくつろいで<数学の部屋<「算数」と「数学」の間で
「算数」と「数学」の間で
最終更新日2010年8月31日
人々の頭を悩ませ続けている算数と数学についてあれこれそれどれ書いています。一応難しい話は抜きで…というつもりで書いています。お茶もお菓子もありませんがごゆっくりお過ごしください。ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
アフィン平面とは何なんだ?その3を加えました。
第1回
第2回 |
ただの数ですが…
ただの数ですが…の続き |
第3回
第4回
第5回
第6回
|
五角形と六角形はどう違う?
五角形と六角形はどう違う?
…の続き
五角形と六角形はどう違う?
…の続きの続き
五角形と六角形はどう違う?
…やっと最終回 |
| 第7回 | 「平均」は平均的? |
第8回
第9回
第10回
| マイナーな数列?カタラン数 マイナーな数列?カタラン数
…の続き もう一つのマイナーな数列?
カタラン数 |
第11回
第12回
第13回 | 紙を折って竜を作る?
紙を折って竜を作る?…の続き
紙を折って竜を作る?…その後は? |
|
|
アフィン平面とは何なんだ?その1
コマ大で2010年3月に放送された「アフィン平面」16個の点を5回折れ曲がる折れ線でつないでいく、という問題でした。解説でアフィン平面の説明をしていましたがおそらく「何が何だかさっぱり分からない」と思われたはずです。今回はアフィン平面とは一体何なのか、ということを書いていきます。コマ大で使われたアフィン平面の定義を書きます。
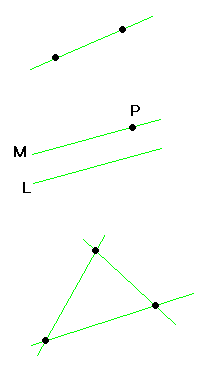 条件1:異なる2点に対して、その2点を通る線がただ1本だけ存在する。
条件1:異なる2点に対して、その2点を通る線がただ1本だけ存在する。
条件2:線LとL上にない点Pに対して、Pを通りLと交わらない線Mがただ1本だけ存在する。
条件3:1本の線の上にない3点がある。
|
番組では「直線」という言葉を使いましたが、ここでは「線」という言葉の方が適しているかもしれません。同じく番組では「Lと平行な…」と書かれていましたが「LとMが交わらない(LとMに同じ点がない)」という表現が適していますので、この表現で話を進めます。
この定義を見て「当たり前だろ」と思った方もいると思います。平面上の点と直線は上の条件を満たします。つまり「平面上の点と直線はアフィン平面」です。ここで「平面上の点と直線」を座標を使って表してみます。
- 平面上の点 ⇒⇒⇒ (x, y) x, y:実数
- 平面上の直線 ⇒⇒⇒ ax + by = c a, b, c:実数、a = b = 0 ではない
簡単ですが、上の1,2,3の性質が成り立つか見てみます。
- 2つの点 (p1, q1), (p2, q2) を通る直線は (q2 - q1) x + (p1 - p2) y = p1 * q2 - p2 * q1
である。(上の式に間違いがありました。訂正します 2010/8/31)
- 点 (p1, q1) を通り、直線 a x + b y = c と平行な直線は a x + b y = a * p1 + b * q1 である。
- 1本の直線の上にない3点として (0, 0), (0, 1), (1, 0) がある。
では「x, y:実数」「a, b, c:実数」の「実数」を他の数の集合に変えるとアフィン平面の性質はどうなるでしょう。
例1:「実数」→「有理数」と変えたとき、アフィン平面の1,2,3の条件をすべて満たします。つまり
- 点:(x, y) x, y:有理数
- 線:ax + by = c a, b, c:有理数、a = b = 0 ではない
という点と線はアフィン平面になります。証明は省きますが、「実数」の場合の証明で出てくる計算がすべて有理数の範囲で済むことで一応アフィン平面になることが分かります。
例2:「実数」→「整数」と変えたとき…はアフィン平面になりません。条件2が成り立ちません。点 (1, 1) を通り、y = 0 と交わらない線は
y = 1, 2x-y = 1, 3x-y = 2
など沢山あります。「後の二つは y = 0 と交わるじゃないか」と思われた皆さん、これらの交点の座標は「整数」ではありません。ですから「y = 0 と 2x-y = 1」や
「y = 0 と 3x-y = 2」は交わらない2本の線の組になります。

例3:「実数」→「複素数」と変えたときもアフィン平面の1,2,3の条件をすべて満たします。つまり
- 点:(x, y) x, y:複素数
- 線:ax + by = c a, b, c:複素数、a = b = 0 ではない
という点と線はアフィン平面になります。こちらも証明は省きます。
以上3つの例を挙げて、アフィン平面になる場合とならない場合を書きました。なぜ
アフィン平面になったりならなかったりするか、というと、実数、有理数、複素数の3つの数の集合は割り算の答えは常にそれぞれの数の集合に入りますが、整数の場合は割り算の答えが必ず整数となるとは限りません(このような性質の数の集合を「体(たい)」と呼んでいます)
3つのアフィン平面の例を挙げましたが、ここでそれぞれの例の「線」のあたるものを調べると次のような関係になります。
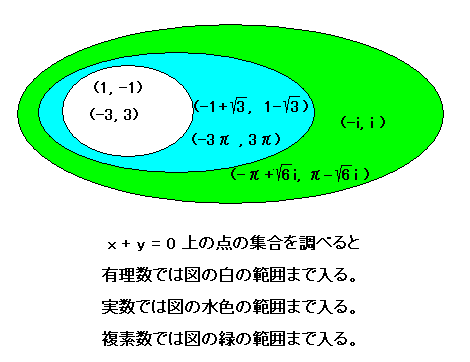
つまり同じ「 x + y = 0 」という線の式でもその線の上の点が増えたり減ったりします。「実数」→「有理数」の場合は直線の所々に穴が空いているような感じです。いっぽう 「実数」→「複素数」の場合は「線」と呼ぶべきかどうか…というような集合になります。
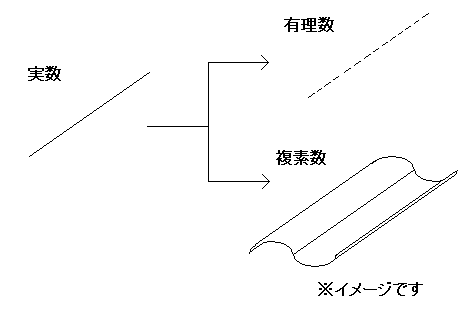
改めて、アフィン平面の定義を見ると、線の性質に「まっすぐである」や「曲がっている」はおろか、線のイメージである「つながっている」や「幅がない」という性質についての話がありません。アフィン平面は「線」というものは「いくつかの点の集合」という性質のみしか考えていません。
ものすごく抽象的な概念です。
しかし、この抽象的な概念を使うと「小さなアフィン平面」というものを作ることができます。「小さなアフィン平面」とは何なんでしょうか?
アフィン平面とは何なんだ?その2
「線」を「いくつかの点の集合」とする、抽象的な概念を使うことでアフィン平面は意外な方向へ進み始めました。上で書いた「小さなアフィン平面」の例を一つご紹介します。
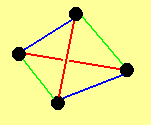 点の集合:四面体の頂点
点の集合:四面体の頂点
線の集合:四面体の辺
|
たったコレだけです。四面体の辺の上には無数の点がありますが、ここでは頂点の2点だけを辺上の点として考えます。本当にアフィン平面になるのか確かめてみます。
- 2つの点を通る線はその2点を通る辺である。
- 一つの線Lとその上にない点Pに対して、Lと交わらず点Pを通る線はLと同じ色のもう一つの辺 である。
- 1本の線の上にない3点として一つの面の3つの頂点がある。
何とも味気ないですが、この通りアフィン平面の3つの条件を満たします。前に書いた「平面上の点と直線」とはまったく違う形をしていながら、これもアフィン平面になります。次に少し大きめの「小さなアフィン平面」(表現は変ですが)の例をご紹介します。
点の集合:図の9個の点
線の集合:図の12本の線

|
「点の集合」は理解できると思いますが「線の集合」の右の二つの図の意味が分かりにくいと思います。それぞれの線を通っている3つの点が「この線の上のすべての点」となります。
最初に書いたようにアフィン平面の「線」は「いくつかの点の集合」という概念しかありません。そのため、これまでのように「線」を直線で表現する代わりに「このような点の集合」という表現をしても問題はありません。
これらの「小さなアフィン平面」は偶然に見つけたものではありません。実はこれらのアフィン平面は上で使われた「平面上の点と直線」の座標表現の「実数」の部分を変えること作ることができます。例えば2番目の例の9個の点のアフィン平面は次のような点と線の表し方で作ることができます。
- 点:(x, y) x, y:0, 1, 2 のいずれか
- 線:ax + by = c a, b, c:0, 1, 2 のいずれか、a = b = 0 ではない
ここで「ax + by = c」という式は「ax + by = c (mod 3) 」という意味で計算をします。(mod 3) とは 3 で割った余りのことを表します。
mod 3 での
足し算
|
| + | | 0 | 1 | 2 |
|
|
|
| 0 | | 0 | 1 | 2 |
| 1 | | 1 | 2 | 0 |
| 2 | | 2 | 0 | 1 |
|
mod 3 での
掛け算
|
| × | | 0 | 1 | 2 |
|
|
|
| 0 | | 0 | 0 | 0 |
| 1 | | 0 | 1 | 2 |
| 2 | | 0 | 2 | 1 |
|
詳しいことはコマ大DVD、第3期「暗号」の回をご覧ください。
この例の場合、点は (0, 0), (0, 1), … (2, 1), (2, 2) の9個あります。
また直線は x = c, x + y = c, x + 2y = c, y = c (c:0, 1, 2) と全部で12本になります。今の場合では「x + 2y = 1」の線の上には (1, 0), (2, 1), (0, 2) の3点があります。これらの点と直線の関係を図で表すと以下の通りになります。
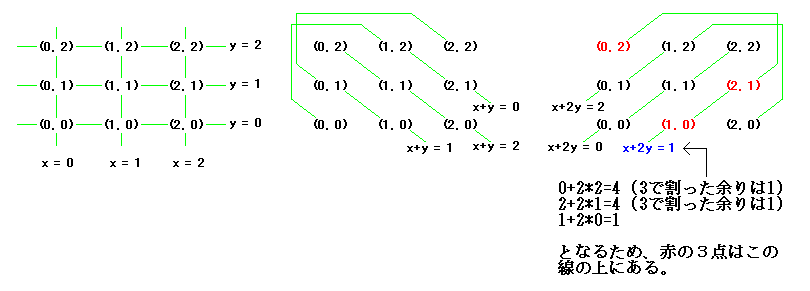
ではこの (mod 3) というものを (mod 2) に変えるとどうなるのでしょうか?
- 点:(x, y) x, y:0, 1 のいずれか
- 線:ax + by = c a, b, c:0, 1 のいずれか、a = b = 0 ではない
この場合の計算は (mod 2) で考えます。
これらの点と線の集合を書き表してみます。(mod 2) と変えてもアフィン平面の性質は変わりません。
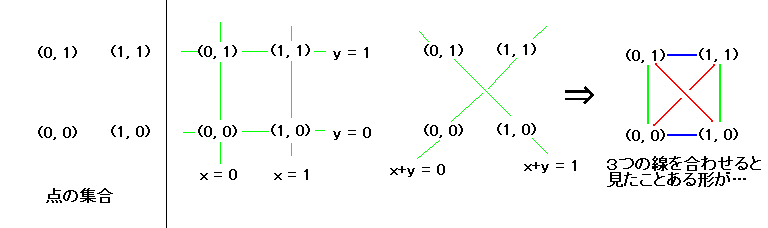
このアフィン平面、実は始めに出てきた「四面体の頂点と辺」からなるアフィン平面と同じものになります。
何度も書きましたがアフィン平面の「線」はこれまでのような平面や空間の中の直線や曲線のイメージではなく、単なる「点の集合」として考えています。そのため、「線」の上の点の数が2,3個しかない場合もありますし、各点が離れた位置にあってもアフィン平面の条件を満たせば「アフィン平面の線」として考えることができます。
さて、(mod 2) や (mod 3) の計算を使って「小さなアフィン平面」を考えましたが、これを (mod 4), (mod 5) …と変えていくとどうなるのでしょうか?この話はまた次回で。
アフィン平面とは何なんだ?その3
「小さなアフィン平面」は (mod 2) や (mod 3) の計算では作ることができました。では (mod 4), (mod 5) …と変えていくとどのような「小さなアフィン平面」ができるのでしょうか?
まず (mod 4) での計算の表を作ります。
mod 4 での
足し算
|
| + | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 1 | 2 | 3 |
| 1 | | 1 | 2 | 3 | 0 |
| 2 | | 2 | 3 | 0 | 1 |
| 3 | | 3 | 0 | 1 | 2 |
|
mod 4 での
掛け算
|
| × | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 0 | 0 | 0 |
| 1 | | 0 | 1 | 2 | 3 |
| 2 | | 0 | 2 | 0 | 2 |
| 3 | | 0 | 3 | 2 | 1 |
|
この計算表を元に、これまでと同様に16個の点と x = a, y = a, x + y = a, x + 2y = a, x + 3y = a という線を作ることができます。この点と直線について調べると次のようなことが起こります。
x = 0 上の点の集合:(0, 0), (0, 1), (0, 2), (0, 3)
x + 2y = 0 上の点の集合:(0, 0), (0, 2), (2, 1), (2, 3)
このように異なる2点を通る線が2本存在することが分かります。これはアフィン平面の条件の1番目「異なる2点に対して、その2点を通る線がただ1本だけ存在する」を満たさないため、この線の作り方ではアフィン平面を作ることが出来ません。この作り方では上の例以外にも異なる2点を通る線が2本存在することがあります。
では、なぜ mod 2, mod 3 の時にはアフィン平面を作ることができたのに、mod 4 ではアフィン平面ができなかったのでしょうか?その原因は上の掛け算の表にあります。
mod 4 での
掛け算
|
| × | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 0 | 0 | 0 |
| 1 | | 0 | 1 | 2 | 3 |
| 2 | | 0 | 2 | 0 | 2 |
| 3 | | 0 | 3 | 2 | 1 |
表の右から2列目の縦の列を見ると、0と2が2個ずつ現れています。他の縦の列は一番左の列を除いて0,1,2,3が1個ずつ現れています。mod 3 の掛け算の表では縦の列は一番左の列を除いて0,1,2が1個ずつ現れています。このことは以前、実数や有理数のアフィン平面の話を書いたときに
実数、有理数、複素数の3つの数の集合は割り算の答えは常にそれぞれの数の集合に入りますが、整数の場合は割り算の答えが必ず整数となるとは限りません
(ただし0で割る場合は省く)と書きました。今回のアフィン平面にならない理由はこの事と似た理由です。申し訳ないですが詳細は省きます。
しかし、この計算の表をちょっと書き換えることによって16個の点からなるアフィン平面を作ることができます。
mod 4 での
足し算
|
| + | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 1 | 2 | 3 |
| 1 | | 1 | 2 | 3 | 0 |
| 2 | | 2 | 3 | 0 | 1 |
| 3 | | 3 | 0 | 1 | 2 |
|
mod 4 での
掛け算
|
| × | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 0 | 0 | 0 |
| 1 | | 0 | 1 | 2 | 3 |
| 2 | | 0 | 2 | 0 | 2 |
| 3 | | 0 | 3 | 2 | 1 |
|
⇒
⇒
⇒
|
新しい
足し算
|
| + | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 1 | 2 | 3 |
| 1 | | 1 | 0 | 3 | 2 |
| 2 | | 2 | 3 | 0 | 1 |
| 3 | | 3 | 2 | 1 | 0 |
|
新しい
掛け算
|
| × | | 0 | 1 | 2 | 3 |
|
|
|
| 0 | | 0 | 0 | 0 | 0 |
| 1 | | 0 | 1 | 2 | 3 |
| 2 | | 0 | 2 | 3 | 1 |
| 3 | | 0 | 3 | 1 | 2 |
|
ご覧の通り掛け算の表を変えましたが、足し算の表も変わりました。さて、これでアフィン平面ができるのでしょうか?
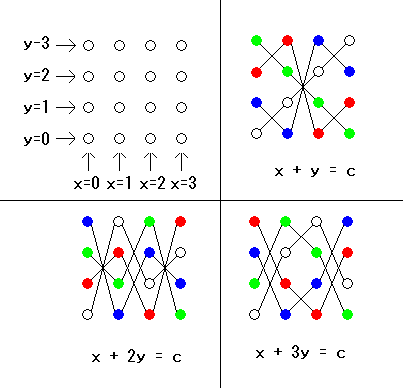 白、青、赤、緑の丸はそれぞれ c=0,1,2,3 の時に通る4点を表す。
白、青、赤、緑の丸はそれぞれ c=0,1,2,3 の時に通る4点を表す。
例えば「x+2y=1」を通る点は
0 + 2 × 3 = 0 + 1 = 1
1 + 2 × 0 = 1 + 0 = 1
2 + 2 × 2 = 2 + 3 = 1
3 + 2 × 1 = 3 + 2 = 1
より、
(0, 3), (1, 0), (2, 2), (3, 1)
(左下の図の青の4点)
の4点である。
|
この図…どこかで見覚えがあるはずです。コマ大の「アフィン平面」のテーマのときに解説で書かれていた謎の図です。放送では解説無しで話をしていましたが、解説を入れるとこんなに長い内容になってしまいます。それにしても何でこんなものを考えたんでしょうかね?
話はまだまだ続きます。これまで mod 2, mod 3 についてアフィン平面を作り、mod 4 の時は表を変えることでアフィン平面を作ることができました。このあと mod 5, mod 6 …と続けていくとどうなるのでしょうか?これについては次の結果が知られています。
| mod n の n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| アフィン平面 | ○ | ○ | △ | ○ | × | ○ | △ | △ | × |
○: mod を使ってアフィン平面ができる
△: 表を変えてアフィン平面ができる
×: アフィン平面ができない
|
不規則に○、△、×が並んでいるように見えますが、これからある法則が見つけることができます。
|
有限個の点からなるアフィン平面(小さなアフィン平面)の点の数は「素数の偶数乗(上の表の n の2乗)」である。
|
小さなアフィン平面の点の数は 2^2, 2^4, 3^2, 5^8 …という形で書くことができます。上の表で見ると「6」のとき点の数は 6^2 = 36 個になりますが、これは「素数の偶数乗」にはなりません。
しかし、この法則必ず成り立つか分かっていません。いわゆる未解決問題です。実際、点の数が 12^2 = 144 個のアフィン平面ができるかできないか今の所分かっていません。たった150個程度の点でも分からないものがあります。番組ではさらりと話していましたが、今回のような奥の深い話が潜んでいたのです。とても30分では解説できないでしょう。
数学とクイズでくつろいで<数学の部屋<「算数」と「数学」の間で