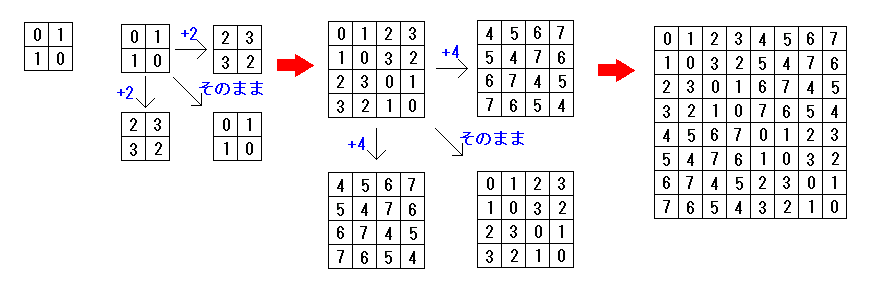
数式で表すと、A 行 B 列に書き込まれる数字は
(（A-2^n) 行 B 列 の数字）+ 2^n (2^(n-1) ＜ B ≦ 2^n ＜ A ≦ 2^(n+1) のとき)
( A 行 (B-2^n) 列 の数字）+ 2^n (2^(n-1) ＜ A ≦ 2^n ＜ B ≦ 2^(n+1) のとき)
(A-2^n) 行 (B-2^n) 列 の数字 (2^n ＜ A, B ≦ 2^(n+1) のとき)
「コマ大数学科」に挑む・１０年１２月
最終更新日２０１１年４月１４日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「数の配列(12/1)」 | |||||
| 「2010年12月コマ大ダイジェスト(12/8〜12/22)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
|
問題：図のような格子状の表の枠内に以下の条件を満たすように０以上の
整数を書き込む。このとき、１１行２２列目に入る数を答えよ。
条件：
|
コマ大チームの検証はいきなりダンカン部長がほかの３人に土下座するところから始まった。なぜ土下座しているのか。今回検証で使うものは「米」…以前検証で米１０００粒と格闘したことがあったため、今回は３人を説得するのに必死であった。再び米との戦いが始まった。
検証は小さな枠の中に、条件を満たす整数を米粒に書き入れ置いていく…という至って地味な作業。米一粒一粒に書き入れていき、やっとで答えを出すことができた。検証を見てマスが一言「米じゃなくてもいいじゃないか！」
確かに…
ま、ともかく答えは出しました。私は検証を見ながらひたすら数字を書いていった（米は使ってませんよ）
|
|
数式で表すと、A 行 B 列に書き込まれる数字は |
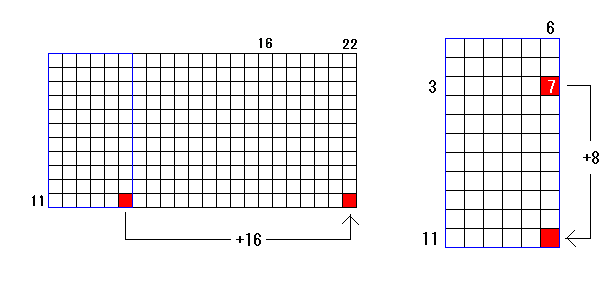A = 11, B = 22 とすると
8 ＜ A ≦ 16 ＜ B ≦ 32 であるため、11 行 22 列 の数字 = (11 行 6 列 の数字）+ 16 A = 11, B = 6 とすると4 ＜ B ≦ 8 ＜ A ≦ 16 であるため、11 行 6 列 の数字 = (3 行 6 列 の数字）+ 8 3 行 6 列 の数字は「7」であったため11 行 22 列 の数字 = ７＋８＋１６ = ３１ |
| コマ大チーム | ３１ | 検証の結果。「３１」と書かれた 米を見せた |
| マス・ポヌペア | ３１ | ２進法に変えて列の一番上と 行の左端の数を足した。 |
| 東大生チーム | ３１ | 行と列の和が 2^n+1 であるとき 2^n-1 が入るということから |
正解…３１、全員正解！
マスは列の一番上と行の左端の数を足して答えを出したが、他の枠の数字の求め方が分からなかった。今回の問題は２進法の「ニム和」を使って書き込む数字を求めることができる。
|
|
というわけで考えました。
今回も解説が長くなりますので別のページに解説を置きました。PDF ファイルですがこちらをご覧ください。難しい理論は使ってないため分かりやすいと思います（２進法のことを知っていれば十分と思います）今回のコマ大フィールズ賞はある程度法則を見つけた、ということから東大生チームに渡った。数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１０年１２月
「2010年12月 コマ大ダイジェスト (12/8〜12/22)」
更新ができなかった間もコマ大を見ていました。一か月ほどは家族の協力でビデオに撮ってもらいました。これまでのように内容を細かく書くことはできませんが、各回の問題・解答・解説、テレビでの内容等について簡単に書いていきます。
「べき級数（12/8）」
|
問題：さいころを二つ振り、合計が偶数か奇数か当てる、ゲームをするとき
普通のさいころと同じ結果になる目の入れ方を求めなさい。
条件： 補足：２個のさいころを投げたとき、出る目の合計のパターンは…
合計２：１通り となる。別のさいころの目の入れ方で上の目の合計のパターンが同じである物を 見つけなさい、ということです。 |
| コマ大チーム | (1,2,2,3,3,4) (1,3,4,5,6,8) | 検証の結果。 |
| マス・ポヌペア | (1,2,3,5,6,7) (1,1,2,2,3,5) | ポヌさんがすべての目の 和の組み合わせから探した。 |
| 東大生チーム | (1,2,2,3,3,4) (1,3,4,5,6,8) | それぞれのさいころに１の目が １個のみ、などの条件から探した。 |
(1,2,2,3,3,4), (1,3,4,5,6,8)
コマ大チーム、東大生チーム 正解！
こちらでご確認ください。
合計２が出るためには、各さいころに１の目が必要。
合計２の目は１通りしか出ないため、各さいころに１の目は２個以上入らない。
============================================================================================
「公務員試験（12/15）」 公務員試験で出題された問題を３問出題した。「公務員の彼氏は？」という質問に東大生チーム小橋・岡本ペアは「夢がなさそう」と一言。
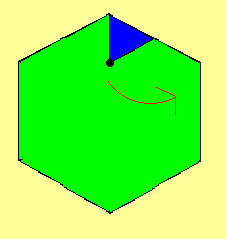問題１：正三角形が、辺の長さが２倍の正六角形の内側を滑らないように
回転するとき、点の軌道はどうなるか？（選択肢は省略。どのような軌道になるか書いてみてください） |
|
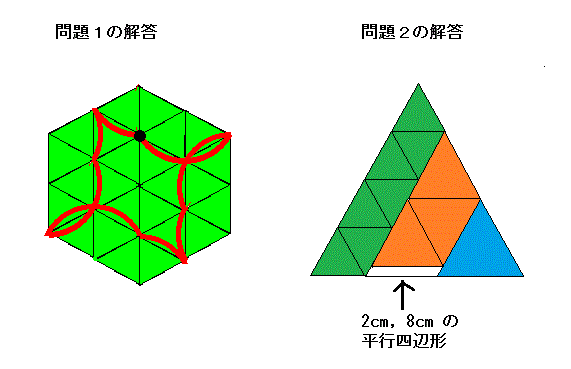
問題２：１辺の長さが６ｃｍの正三角形が７枚、８ｃｍの正三角形が３枚、１０ｃｍの正三角形が１枚ある。 これらにあと１枚ある形を加えることで、１辺の長さが２４ｃｍの正三角形を作ることができる。加えるあと１枚は次のうちどれか？
|
|
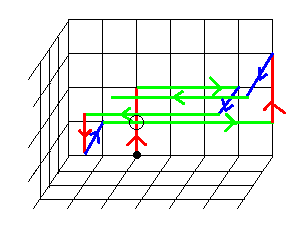
問題３：ヘリコプターが以下のように移動したとき、同じ地点を何回通過するか？
200m 上昇 → 300m 東へ進行 → 200m 南へ進行 |
| コマ大チーム | １回 | 検証の結果。 |
| マス・ポヌペア | １回 | 図を使って答えを出した。 |
| 東大生チーム | ０回 | こちらも図を使って 答えを出したが… |
正解…１回 コマ大チーム、マス・ポヌペア 正解！
この問題は実際に図を書いていくと答えが見えてくる（下の図の丸印の箇所が通過する所）
============================================================================================
「クオリティコントロール（12/22）」 「クオリティコントロール」とは「品質管理」のこと。いかにコストを抑えて品質を管理できるか、に関する問題。
|
問題：１個販売すると１０００円の利益を得られる製品が１１個ある。しかしその中の１個は不良品が入っていることが分かっている。機械を使い、以下の方法で製品の良品・不良品を判定する。
|
（判定の途中で不良品が見つかった場合、それ以降の調べていない製品は販売に回すことができる。
また、最後の段階を残して不良品が見つからない場合は、最後の中に不良品が入ることが分かるため、
機械を使わなくてよいが、すべて販売に回せない）
例： 費用をおさえて、調べる機械の回数を減らすこともできる。しかし、一度に調べる製品の 個数も増えるため、不良品が出たときに販売に回せない良品も増える。 |
| コマ大チーム | ５個，３個，１個の順で 利益５０００円 | 検証の結果。 |
| マス・ポヌペア | ４個、３個、２個、１個の順で 利益６０００円 | 場合分けをして利益を計算。 |
| 東大生チーム | ４個、３個、２個、１個の順で 利益６０００円 | こちらも場合分けをして利益を計算。 |
正解…４個、３個、２個、１個の順で
利益６０００円
マス・ポヌペア 東大生チーム正解！
私は「均等に分ける方が良い」と考え「３個、３個、３個、２個」などを考えていた。最後を１個にした方が良いことに気が付いたのはタイムアップぎりぎりであった。コマ大フィールズ賞は早さで勝ったマス・ポヌペアに渡った。
数学とクイズでくつろいで＜数学の部屋＜「コマ大数学科」に挑む＜「コマ大数学科」に挑む・１０年１２月
