3×3のマス目に1〜9の整数が一つずつ書かれています。
各縦の列の3つの数の中で2番目に大きい数にそれぞれ印を付けます。 印の付いた3つの数の中で2番目に大きい数が5になりました。
このような、9個の整数の配置として考えられるものは何通りあるでしょうか?

「コマ大数学科」に挑む・11年9月
最終更新日2011年10月27日
フジテレビで深夜に放送されている「コマ大数学科」の問題に解く様子をご紹介します。数学をやってきたので簡単に解ける…と思ったものの…その奮闘振りをお楽しみに。なお、福岡での放送は二週間遅い模様です。そこら辺はご勘弁を。| 「数オリなでしこジャパン (9/7)」 | |||||
| 「メンサに挑戦 (9/14)」 | |||||
| 「L (9/21)」 | |||||
| 「片恋慕四巴戦 (9/28)」 |
ご意見がありましたらtfujisaki2006@yahoo.co.jpまでお願いします。
「数オリなでしこジャパン (9/7)」
|
問題: 3×3のマス目に1〜9の整数が一つずつ書かれています。 各縦の列の3つの数の中で2番目に大きい数にそれぞれ印を付けます。 印の付いた3つの数の中で2番目に大きい数が5になりました。 このような、9個の整数の配置として考えられるものは何通りあるでしょうか?
|
|
問題: 3×3のマス目に1〜9の整数が一つずつ書かれています。 各縦の列の3つの数の中で2番目に大きい数にそれぞれ印を付けます。 印の付いた3つの数の中で2番目に大きい数が5になりました。 このような、9個の整数の配置になる確率を求めなさい。 |
今回の問題はマスも東大生もある程度の解き方が分かったようであったが、先に答えを出したのは東大生。マスは苦戦し、東大生の答えをカンニング……
| コマ大チーム | 2/3 | 9回の検証で6回条件を満たした。 |
| マス・ポヌペア | 2/7 | 1〜4,5,6〜9に分けて考えた。 |
| 東大生チーム | 4/7 | 1〜4,5,6〜9に分けて考えた。 |
正解…4/7 東大生チーム正解!
今回は見事な解説を見せた東大生チームにコマ大フィールズ賞が渡った。この問題は5と同じ列に入る残り2つの数を考えれば簡単に答えを出すことができた。
|
5に印が付くとき、5と同じ列に入る残り2つの数のうち
1つは5より小さい(1〜4のいずれか、図の青の数) このとき、残り2列の数の配置は次のいずれかである。 ・1列は5より小さい3個の数、もう1列は5より大きい3個の数(例:下左の配置) ・1列は5より小さい2個と大きい数1個、もう1列は5より大きい2個と小さい数1個(例:下右の配置)
|
2つの場合、いずれでも印の付く3つの数字の中で2番目に大きい数が5になることが分かる(つまり印の付く数の1個は5より小さく、もう1個は5より大きい) つまり、5に印が付いたら必ず印の付く3つの数字の中で2番目に大きい数が5になる。よって5に印が付く数の配置を考えればよい。 5に印が付く数の配置は以下の方法で計算することができる。
・5が入る位置が9通り。 以上から5に印の付く数の配置の個数は「9×16×2×720=207360通り」となる。 1〜9の数字を入れる配置の個数は1×2×…×9通りあるため、求める確率は 9×16×2×720/1×2×…×9 = 4/7 となる。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年9月
「メンサに挑戦 (9/14)」
まずはメンサの人達とはどのような人達なのか、コマ大チームがメンサ日本支部の会長、副会長の二人に会いに行った。会長はいたって普通の方だったが、副会長はロックバンドのヴォーカルを務める人で金髪にメイク、皮のジャケットの姿で登場。この副会長とコマ大チームチーム・ガンビーノ小林が対決した。
|
第1問: 次の数列の?に入る数字を答えなさい。 7→14→11→18→15→? |
|
第2問: 以下の対応から、?に入る数字を答えなさい。 あ=1、き=4、せ=12、と=20、ひ=? |
|
第1問の解答: 次の数字との差を見ると+7、−3、+7、−3…と繰り返されているため、次は+7の差であるため22が正解。 |
|
第2問の解答: 五十音の行「あ〜わ」に「1〜10」、段「あ〜お」に「1〜5」と数字を対応させる。 ひらがなの行と列に対応する数字を掛け合わせると問題の数字が出てくる。例えば 「あ」は「あ行のあ段」であるため「1×1=1」、「せ」は「さ行のえ段」であるため「3×4=12」 「ひ」は「は行のい段」であるため「6×2=12」が正解。 |
|
第3問: 下の菱形の図形を四つの同形の図形に分解しなさい。ただし図の〇、△、□の記号は 各図形に一つずつ入るようにすること。
|
|
左から、コマ大チーム、マス・ポヌペア、東大生チーム、副会長の解答。
|
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年9月
「L (9/21)」
|
問題: 図のようにL字の形をした図形に直線を引き面積を三等分するとき、?の部分の長さを求めなさい。
|
東大生チームは木村・山田ペア。スタジオには初代東大生チームの松江さんが遊びに来ていた。このほど結婚し名字が「木村」に変わる、とのこと。その結婚相手とゆっくりと番組を見ているかと思いきや、同じ問題を解き始めた。今回はしっかりと計算を進めて答えは出たのでしょうか?
| コマ大チーム | 8cm | 一言「目分量」 |
| マス・ポヌペア | 6cm | 三角形の比を使い計算。 |
| 東大生チーム | 7cm | 斜めの線を修正して面積を 計算した。 |
| 木村夫妻 | 6.8cm | 解説は無し |
正解…6.8cm 木村夫妻正解!
東大生チームの解説も間違ってはいなかったのですが、最後の計算で間違えてしまいました。それでは解説。
|
図のように図形の中心を通る線を引き、その線と赤線との交わりから垂直な線で図形を分割すると、 青の三角とピンクの三角は合同であることが分かる。このため2本の垂直な線はL字の図形を同じく3等分していることが分かる。 上と右の図形は長方形であるため、面積から各辺の長さが上の図の通りに求められる。また残りの図形の各辺の長さも求められる。 |
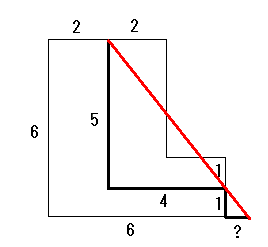 赤の斜線はL字の両端の中点を通るため、右の図の直角三角形を考えると2辺の長さは縦5、横4となる。下の小さい直角三角形はこの直角三角形と相似であるため。
赤の斜線はL字の両端の中点を通るため、右の図の直角三角形を考えると2辺の長さは縦5、横4となる。下の小さい直角三角形はこの直角三角形と相似であるため。5:4=1:? ⇒ ?=4/5=0.8 となる。よって全体の長さは6+0.8=6.8cmである。 |
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年9月
「片恋慕四巴戦 (9/28)」
|
問題: Aくん、Bさん、Cくん、Dさんの4人が1辺5mの正方形の頂点にいます。 AくんはBさん、BさんはCくん、CくんはDさん、DさんはAくんがそれぞれ好きでそれぞれ相手に向かって走り、相手の動きに合わせて進行方向を変えて近づいていきます。 最終的に4人はどれだけの距離を走るでしょう
|
東大は試験期間、ということでしょうか今回の東大生チームは木村・杉山の混成ペア。一方ポヌさんも試験でお休みのためマスは一人で問題に挑む。混成ペアの実力はいかに、と思いきや問題の正方形の上に4本の鉛筆で走ったコースを書き始めた。マスも同じ要領でコースを書くが問題はその距離。どのように求めたのでしょうか?
| コマ大チーム | 4人とも4m15cm | 検証の結果 |
| 東大生チーム | 4人とも5π/2m | 半径5の円周の1/4位と考えた |
| マス北野 | 4人とも5m | 円の一部をつなぎ合わせるとこの位、と推測 |
正解…4人とも5m マス北野正解!
見事なマスのひらめきである。この問題はちょっとしたひっかけ問題でした。走るときの4人の位置を考えると、正方形の四隅にいて次第に小さくなっていく形になります。つまりそれぞれの人が5mの距離を縮めるように走るため4人とも5mずつ走ることになります。もう少し数学的な解き方がないのか、ということで正確な解法ではありませんが以下のような解法もあります。参考にしてください。こちらです。 今回のコマ大フィールズ賞は文句なしマス北野に決定。
数学とクイズでくつろいで<数学の部屋<「コマ大数学科」に挑む<「コマ大数学科」に挑む・11年9月